VOL.115【場合の数攻略】　－まとめ－

最近は海外に活躍の場を求める人が増えてきているように思います。

スポーツの世界でもメジャーリーグで当たり前のように活躍する選手がいますし、サッカーの超名門チームと契約した１０代の選手もいます。

アメリカの弁護士の資格を取る人もいれば、海外に飲食店をオープンする人もいます。

昔から道は拓けていたのかもしれませんが、我々の時代はチャレンジしようという発想そのものがあまりなかった気がします。
今の若い人たちは活躍の場がたくさんあり、そういった意味では羨ましい限りです。

ただし、海外で活動するためには、言葉の問題をクリアしなければならないこと。
また、ライバルが世界中にいるとも考えられることには注意しなければなりません。

いずれにせよ私たちは世界に通用する人材の育成という意識を持って、子供たちを指導していかなければならないと考えています。

さて、【場合の数攻略】も今回が最後となりました。まとめていきたいと思います。

①「場合の数」の特殊性

当たり前ですが、入学試験で大切なことは点数を取ることです。
問題を解いて点数を取るということは、「時間を点数に変えること」と捉えることができます。

このように考えると、試験で一番まずいのは「時間をかけたが得点できなかったケース」であると言えます。
そしてそうなる可能性が最も高い分野が「場合の数」なのです。

なぜそうなるかというと、ひとつは検算のしにくさにあると思います。
これが「文章題」であるならば問題文の条件に当てはめて確認することができますし、「図形」ならば見た目を判断材料にすることができます。
ところが「場合の数」はいったいどれぐらいになるか見当もつかなかったりします。

例えばＶＯＬ．１１２の＜例題１＞にしても、少し条件が変わっただけで答が６・１２・２７（通り）と異なってきますし、＜例題３＞は、おおよそ何通りになるのかのイメージがなかなか湧かないことでしょう。

また、「場合の数」には罠のようなものが潜んでいることも多いです。
同じくＶＯＬ．１１２の＜例題２＞がその例で、集中力を欠けばすぐにダブってしまうことでしょう。
そのほかにもＶＯＬ．１１３の＜例題３＞がダブってしまい、＜例題４＞が見落としてしまうことが多い例です。

以上見てきたように「場合の数」は「危険」な分野です。

いきなり得点源にしようとはせず、基本からコツコツと積み上げていくことをお勧めします。
そして本番では決して深追いしないことが肝心となります。

②「書き出し」と「計算」のバランス

これはどれだけ深い学習ができているかで変わってきます。
できれば「計算」で解きたいのですが、学習の深さが中途半端だと、必ずといって良いほど間違えます。
ですから普段の学習で自分がどのレベルの問題までなら「計算」でサッと答を出せるかを掴んでおき、それよりも難しいものに関してはまず「書き出し」というバランスを身に着けたいところです。

また、①で「検算」のしにくさについて書きましたが、「計算」と「書き出し」で答が一致したならば、それが正解である可能性はかなり高いと言えます。
そういったことからも「計算」と「書き出し」のどちらかに偏るということがないように注意し、それぞれの解法の長所を生かせるようになりたいですね。

③問題文の読み取り　～タイプを見抜く～

ＶＯＬ．１１２で「問題文の読み取り」について詳しく解説しましたが、「国語力」の重要性について理解していただけたでしょうか。
「算数」が担当する「問題文の読み取り」は、自分のフィールドに引っ張り込む部分で、必要に応じて手を動かす（書く・描く）べきであることは書きました。

さて、問題文が何を言っているのかがわかった後ですが、どのようなタイプかで分類する必要があります。以下にいくつか例を挙げます。

◎「順列」「組み合わせ」の計算で処理できるタイプ（工夫して持ち込めるものも含む）

＜例題１＞
Ａ、Ｂ、Ｃ、Ｄ、Ｅの５人が真横に並ぶときＡとＢがとなり同士になるような並び方は何通りありますか。

＜解答１＞
Ａ、Ｂを１人とみなします。
｛Ａ，Ｂ｝と｛Ｂ，Ａ｝の並びがあるので２倍します。
４×３×２×１×２＝４８（通り）　…（答）

◎「場合分け」をすればそれぞれが「基本問題」となるタイプ

＜例題２＞
４、５、５、６、６の５枚のカードがあり、この中から３枚を選んで３桁の数をつくります。
６のカードは９としても使えるとき３桁の数は何種類つくることができますか。

＜解答２＞
場合分けをします。

i）５、６ともに１枚使い→（４，５，６）と（４，５，９）
３×２×１×２＝１２（種類）

ii）５を２枚使い
３×３＝９（種類）
→４５５，５４５，５５４，６５５，５６５，５５６，９５５，５９５，５５９

iii）６を２枚使い
①６６　９９
３×２×２＝１２（種類）

②６９→（４，６，９）と（５，６，９）
３×２×１×２＝１２（種類）

以上より
１２＋９＋１２＋１２＝４５（種類）

◎前の結果を利用するタイプ

＜例題３＞
「○」か「×」のどちらかの記号を真横に８個並べるとき、何通りの並べ方がありますか。
ただし「○」は３個続けては並べることができず、「×」は２個続けては並べることはできないものとします。

＜解答３＞
２番目以降の最後の２個で分類した表を作ります。

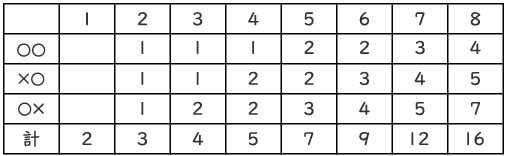
（答）１６通り

◎余事象が利用できるタイプ

※余事象についてはＶＯＬ．４の今週の１題の解説を参照のこと

＜例題２の別解＞
４，５，６，９が３枚ずつあったならば
４×４×４＝６４（種類）
つくることができますが、ここからつくれないものを引きます。

i）３つ同じ
４種類

ii）６６９、６９９
３×２＝６（種類）

iii）４を２枚使い
３×３＝９（種類）

以上より
６４－（４＋６＋９）＝４５（種類）…（答）

※＜例題２＞は余事象を利用して答を出し、時間に余裕があったら場合分けをして検算するというやり方がベストでしょう。

◎表が安全確実なタイプ

＜例題３＞
さいころを２個ふるとき、２つの目の積が６の倍数になる確からしさを求めてください。

＜解答３＞
表をつくります。

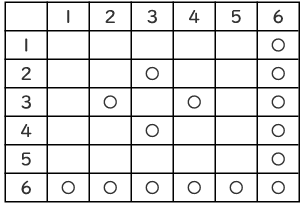
表より

１５ ６×６  ＝ ５ １２  …（答）

④他分野との融合

ＶＯＬ．１１３で「図形」との融合について詳しく書きましたが、それ以外にも「数の性質」や「規則性」（ＶＯＬ．１１０がその例）との融合問題も視野に入れておく必要があります。

いずれにしても「分野」における「苦手」は致命傷となりかねませんので、「基本」は十分に身に着けておかなければなりません。

「算数」は分野ごとに学習を進めていくのが普通です。
しかし、最終的にはその分野の垣根が取払われていくようなところがあります。
そのようなレベルに到達したならばきっと「算数」は得意科目になっているでしょうし、最後の難関である「場合の数」の攻略に目処が立ったと言えるのではないでしょうか。

具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。