VOL.342〈分野別〉知識の確認2 ― 規則性 ―
前回から始まったこのシリーズ,今回は規則性をやります。
規則性は正解することが特に重要な分野なので,「知識」の重要性も高いと考えています。そのあたりのことも考慮して今回も3つの題材を選びました。
それではスタートしましょう!
「初級」
◎等差数列のN番目の項は【 公差×N±□ 】であらわすことができる。
〈例題〉
初項が3,公差が13の等差数列があります。この数列の20番目の項を求めてください。
〈解説〉
この数列の第N項は
13×N-10
で求められるので
13×20-10=250…(答)
※公式は
第n項=初項+公差×(N-1)
です。これを使うと
3+13×(20-1)
=3+13×19
=3+247
=250
とやる流れになり,若干損しているというか,ミスの可能性が上がっているように思います。
「中級」
◎N番目の三角数 と (N+1)番目の三角数 の和は,(N+1)番目の平方数 になる。
〈例題〉
1番目から100番目までの三角数100個を全て足してものを2倍した数をAとします。また1番目から100番目までの平方数を全て足した数をBとします。AとBではどちらがいくつ大きいですか。
〈解説〉
1番目から100番目までの三角数に1番目から99番目までの三角数を加えると,1番目から100番目までの平方数になるので,Aの方が100番目の三角数の分だけ大きいことになります。
よって
(1+100)×100÷2=5050
より
Aのほうが5050大きい…(答)
筆算であらわすと以下になります。
1+3+6+10+…+5050
+ 1+3+ 6+…+4950
1+4+9+16+…+10000
※なぜそうなるのかは明らかだと思います。
例 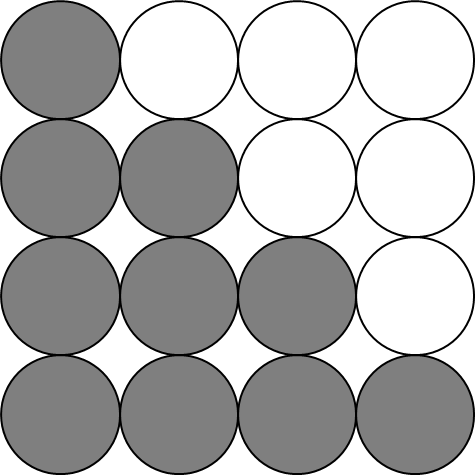
白が3番目,黒が4番目の三角数。和は4番目の平方数。
「上級」
◎前の結果を利用するタイプの場合,表に整理すると良い。
〈例題〉
下の《図》のように,中央に穴の開いた大きさの異なる円盤5枚が,3本ある棒のうちの一番左に下から大きなものから順に重ねられています。
以下の〔ルール〕に従ってすべての円盤を右端の棒に移動させるには最も少なくて何回の移動が必要ですか。
〔ルール〕
・円盤を一回に一枚ずつどれかの棒に移動させることができる。
・小さな円盤の上に大きな円盤を乗せることはできない。
《図》

〈解説〉
円盤を小さいほうからA,B,C,D,Eとします。Eを右端に動かす際は中央の棒に上からA,B,C,Dの順に4枚なければなりません。そこまでは4枚を違う場所に持っていくだけの手順が必要です。そして,Eを右端に動かした後も4枚を違う場所に持っていく手順が必要ですから,N枚を違う場所に動かすために必要な最小の手順は「N枚より1枚少ないときの手順の2倍より1大きい」ので
〈N-1〉×2+1 (〈N〉はN枚を違う場所に動かすために必要な最小の手順)
となります。
これを表にまとめると
| N | 1 | 2 | 3 | 4 | 5 |
| 手順 | 1 | 3 | 7 | 15 | 31 |
表より
31回…(答)
〇表にまとめると良いものをいくつか挙げておきます。
【フィボナッチ数】
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 項 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
【トリボナッチ数】
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 項 | 1 | 1 | 2 | 4 | 7 | 13 | 24 | 44 | 81 | 149 |
【ペル数】
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 項 | 1 | 2 | 5 | 12 | 29 | 70 | 169 | 408 | 985 | 2378 |
※それぞれどのような規則性なのかは各自で考えてみてくださいね。
いかがでしたでしょうか。
上手く知識を活用できれば,考える時間や計算量を減らすことができます。皆さんが「時短」と「ミスとの決別」を実現し,規則性を得意分野にすることを期待しています。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題数と規則性
難易度★★★★☆
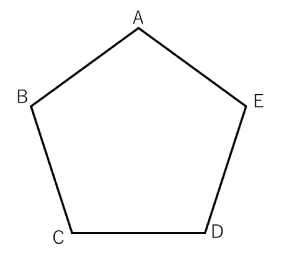
〈図1〉は正五角形です。点Pは正五角形の頂点の上をサイコロの目に応じて動きます。
最初Pは,頂点A上にあり,サイコロの目が奇数なら反時計まわりに,偶数なら時計まわりに,その目の数だけ動きます。
例えばサイコロを2回ふり「2」,「3」の順に出たとすると,Pは頂点D,頂点Bと動きます。
〈図1〉
(1)サイコロを3回ふってPが頂点Cにあるようなサイコロの目の出方は何通りありますか。
(2)サイコロを5回ふってPが初めて(スタート時は除く)頂点Aにあるようなサイコロの目の出方は何通りありますか。
解答が表示されます













