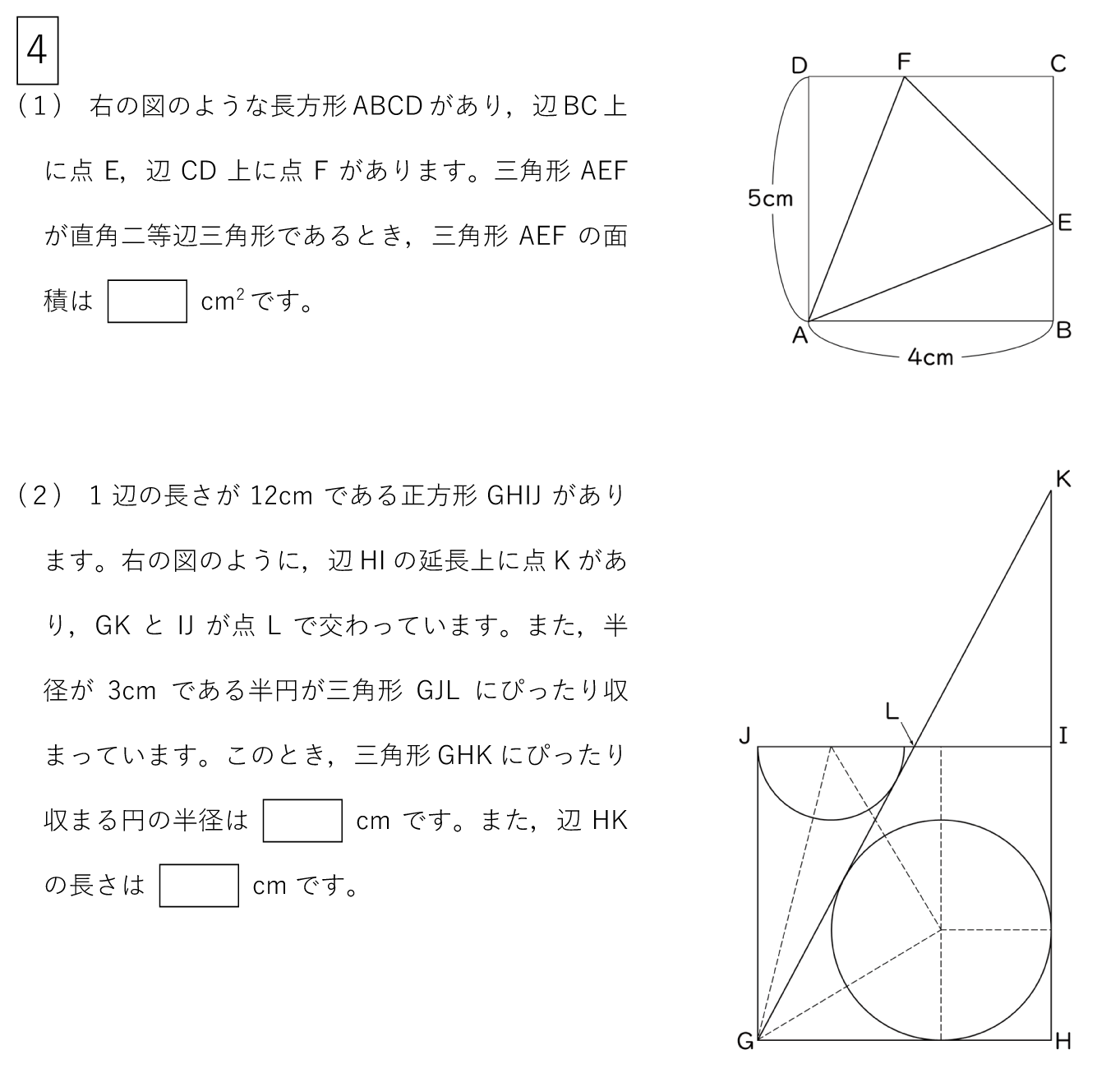
VOL.338【新シリーズ】　― 中受流証明４ ―

今回は灘２日目の問題を題材として中受流証明をやってみたいと思います。
まずは問題を見てください。今年の４番です。

何を証明するかというと，(２)の左の方にある三角形が直角二等辺三角形であることです。

実際の入試では証明を要求されているわけではないので，「直角二等辺三角形」と決め打つ方が得策だった可能性が高いですが，時間の余裕がある今はしっかり学ぶとしましょう。

(１)を普通に解き，それを利用して証明を行い，おまけで(２)を解くことにします。

〈解説〉

(１)　△AEFが直角二等辺三角形ということは∠Eが直角ですからAE＝EFになります。
また，∠AEFが90°なら
∠AEB＋∠FEC＝180°－90°＝90°
また
∠AEB＋∠EAB＝90°
なので
∠EAB＝∠FEC
よって直角三角形の合同条件を満たすので
△ABE≡△ECF(斜辺１鋭角相等)
CE＝4cm
EB＝1cm
DF＝3cm
求める面積は
5×4－(5×3÷2＋4×1÷2×2)＝8.5(cm²)･･･(答)

〈証明〉

〈図１〉

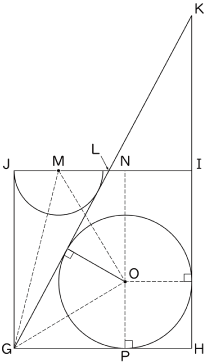
〈図１〉は(２)の図中の点に名前をつけたものです。内接する半円の中心がM，内接する円の中心がOです。このとき，△MGOが直角二等辺三角形になることを証明します。

〈図２〉は(１)の図に点Eから辺AFに垂線を下ろし，その交点Qを通る長方形RSECを作図したものです。
仮に〈図１〉の△MGOが直角二等辺三角形であるならば，長方形JGPNは〈図２〉の長方形RSECを裏返して３倍に拡大したものになります。

〈図２〉

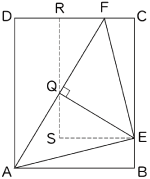
RQ＋QS＝4(cm)
SE－RF＝RQ－QS＝1(cm)
より
RQ：RF＝(4＋1)：(4－1)＝5：3

よって〈図１〉の△MNOの辺NOと辺NMの長さの比が5：3なら△MGOが直角二等辺三角形になります。

以下NO：NM＝5：3であるものとして進めます。
NO＋NM＝NO＋OP＝12(cm)･･･①
NO－NM＝PG－NM＝3(cm)
NO＝(12＋3)÷2＝7.5(cm)
NM＝12－7.5＝4.5(cm)＝OP
また
GP＋PH＝12(cm)･･･②

①②より
OP＝PHとなるのでOは確かに内接円の中心になっています。

以上より
△MGOは直角二等辺三角形です。　　〈証明おわり〉

(２)　最初の□に入るのは4.5･･･(答)です。

〈図３〉

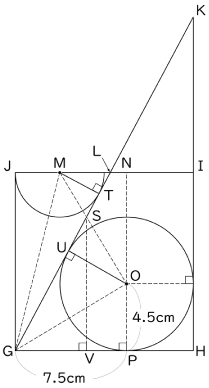
〈図３〉は〈図１〉に補助線を加え点に名前をつけたものです。点Mと点OからそれぞれLGに垂線を下ろし，その交点をTとＵとします。また，LGとMOの交点をSとし，SからGHに下した垂線との交点をVとします。
〈図３〉で
△MST∽△OSU(２角相等)
その相似比は
MT(半円の半径)：OU(円の半径)＝3：4.5＝2：3
よって
MS：SO＝2：3
となります。

ここで△KGHと相似である△SGV(２角相等)のSVとGVの長さを求めます。

SV＝4.5＋7.5×  ３  ２＋３  ＝9(cm)
GV＝7.5－4.5×  ３  ２＋３  ＝4.8(cm)
よって二番目の□である
辺HK＝12×  ９  4.8  ＝22.5(cm)･･･(答)

いかがでしたでしょうか。

証明方法はほかにも色々とありそうですが，紹介した方法がなかなか面白かったので，今回採用しました。
算数は楽しみながら学習できると，どんどんできるようになりますよ！