VOL.112【場合の数攻略】　－問題文の読み取り－

芸能人が大学受験に挑戦する番組が、いままで何回か放送されてきました。
結果は大抵の場合うまくいっていないようですが、先日放送されていた番組では最難関大学の足切りラインは突破していました。

私もたまに見ていたのですが、注目したのは、「国語」重視だったことと、半年弱の準備期間で結果が出やすかったのは「文系科目」だったことです。

「国語重視」の理由ですが、
『問題が日本語である以上、「国語」は全ての科目の基礎になる』
といったことでしたが、まさにその通りだと思います。
そしてそのことは「中学受験」にも当てはまります。
それどころか、影響力の度合いからいったら「大学受験」よりも大きいと言えるかもしれません。

「理系科目」苦戦の原因ですが、大人と言えども「覚える」だけではダメで、「練習」が必要なことが考えられます。
ただ、一旦身に着けてしまえばその後はあまり時間が必要にならないかもしれませんから、準備期間が長ければ理系科目での苦戦は減ると思われます。
要は『「数学」は１からやるには「半年」では短すぎた』ということでしょう。

これもまた、「算数」に当てはまると思います。
「受験勉強」の開始時期がどんどん早まっているのは「算数」の難化と無関係ではないでしょう。

今回のテーマは、「問題文の読み取り」です。
「場合の数」に限ったことではないですが、ここが弱い受験生は「点数」が取れないので、なるべく早い時期に解消したい問題だと思います。

まず、「言語」と「計算」の関係について考えてみます。

「計算」も「言葉」がわからなければ処理は難しいと思うのです。
「１＋１＝」を頭のなかで「イチ足すイチは」とやっているわけです。
つまり、「計算」と言えども、一度は「日本語」を介して頭を働かせているように思うのです。
実際、バイリンガルは計算によって使う言語を変えることもあるという記事を読んだことがあります。

計算するにも「日本語」が必要なので、これがもっと複雑な問題なら、益々「言葉」に頼らなければならないであろうことは容易に想像できます。

「中学受験」でこのことが問題になるのは主に「数量」の分野です。
特に「文章題」「場合の数」では設定が複雑になることが多く、対策を講じておく必要があるでしょう。

この手の「読み取り」が苦手な受験生の対策として「国語力強化」が考えられます。
私は「算数」担当ですが、
『名門会の「国語」の先生にみてもらったらもっと伸びるのに』
と思うことがよくあります。
「国語」も「算数」と同様、「集団授業」の効果に個人差が出やすい科目であり、ましてや「算数」の問題の読み取りに難があるようなレベルであれば「集団授業」の効果はあまりない可能性が高いでしょう。

こういった受験生においては「個別指導」による「問題の読み取り」の強化を強くお勧めします。

「国語」だけに頼るわけにもいきませんから、具体例を挙げながら対策を考えてみましょう。

＜例題１＞

〈図１〉のような長方形を３分割したそれぞれの部分を、赤・青・黄の３色のどれかで塗るとき、何通りの塗り方がありますか。

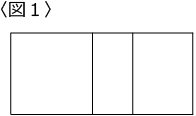
＜解説１＞

これと同じ問題は意外と少ないかもしれません。
どの問題集にものっている基本問題は「塗る」が「３色を全部使って塗り分ける」になっているものが多いです。
単に「塗り分ける」なら
３×２×１＋３×２＝１２（通り）
ですし、「３色を全部使って塗り分ける」なら
３×２×１＝６（通り）
が答ですが、この問題の場合は「赤・赤・赤」や「赤・赤・青」でも良いので
３×３×３＝２７（通り）
が正解となります。
このあたりをきちんと読み取るためには普段から言葉の意味を意識しておく必要があるでしょう。

この問題はちょっとした「言葉」の違いが答に影響する例でした。

＜例題２＞

色が赤と青と黄の布が３枚ずつあります。
大きさ・形はどれも同じで２０ｃｍ×１０ｃｍの長方形です。
この布を３枚つないで長方形の旗を作るとき、布の部分だけを考えた場合、何種類の旗を作ることができますか。
ただし、布と布のつなぎ目は無いものとし、布の表と裏は区別できないものとします。

＜解説２＞

作れる長方形は６０ｃｍ×１０ｃｍと３０ｃｍ×２０ｃｍですが、後者はつなぎ方が２種類あります。
さて、この問題は「同じ旗」とはどういうことなのかをきちんと捉えないと正解できません。

①回転して同じになるものは１種類と数える

上の２つは同じです。

②裏返して同じになるものは１種類と数える

上の２つは同じです。
※ここまでは、旗の「布の部分だけ」を考えると書いてありますから、間違えてはいけません。

③つなぎ目が異なっても色が同じなら１種類と数える

上の２つは同じです。
「つなぎ目はないものとし」とありますから、ここは気づかなければなりません。

以上を踏まえ場合分けをします。

i）６０ｃｍ×１０ｃｍ

ア）１色の場合

３通りです。

イ）２色の場合 → 2つに場合分けします

３×２＝６（通り）

３×２＝６（通り）
よって
６＋６＝１２（通り）
ウ）３色の場合
真ん中が決まれば自動的に決まるので、
３通り。

ア）～ウ）を合計すると、
３＋１２＋３＝１８（通り）

ii）３０ｃｍ×２０ｃｍ（１）

ⅰ）と同じなので１８通り。

iii）３０ｃｍ×２０ｃｍ（２）

ア）１色の場合

ⅱ）で数えてあるので０通りです。

イ）２色の場合

ⅱ）で数えてあります。

３×２＝６（通り）

ウ）３色の場合

長方形が縦になっている部分が決まれば全体も決まるので３通り。

ア）～ウ）で、ⅱ）で数えていないものを合計すると、
６＋３＝９（通り）

以上を合計して　
１８×２＋９＝４５（通り）　…（答）

設定が複雑な問題で罠が沢山仕掛けられています。
それらに全て気づきましたか。
気づくかどうかのポイントの一つに「言葉に対する反応」があったと思いますが、どうだったでしょう。

＜例題３＞

〈図２〉のような８個のマス全部に〇か×の記号を入れます。
どのマスについても隣り合っているマスのうち少なくとも１つに〇が入っているような〇と×の入れ方は何通りありますか。

＜解説３＞

このレベルになると何を言っているのか瞬時にはわからない受験生もいるでしょう。
ただ焦る必要はありません。
落ち着いて調べていきましょう。
「どのマスについても」とありますから漏れがないようにしないといけません。

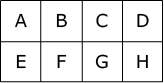
上のように場所に名前をつけました。
まずはＡについて考えてみます。
隣り合っているのはＢとＥでそのうち少なくとも１方には〇が入っているということがわかります。
またＨについてみればＤかＧのうちのどちらかに〇がはいっていることがわかります。
そうするとＣとＦについては、Ａ・Ｈに関して条件を満たしていれば大丈夫ということになります。
｛Ｅ，Ｂ｝→｛〇，〇｝｛〇，×｝｛×，〇｝…３通り
｛Ｇ，Ｄ｝も同様に３通り

上の黒い部分の〇×の入れ方
３×３＝９（通り）
同様に白い部分の入れ方も９通り。
よって求める答は
９×９＝８１（通り）
となります。

少し考えにくかったかもしれませんが、解説を読めば理解できたと思います。
この問題は「言葉」に反応していかに手を動かすことができたかがポイントだと思います。

今回は「問題文の読み取り」をテーマにしましたが、まずは「国語力」の強化が大切です。
そして、問題を解く際はまず「問題文をよく読む」こと、つまり集中して、勘違いなどがないようにしなければなりません。
さらに、そこから先の「考える」ということに結びつけていかなければならないので、そのつなぎ役として「手を動かす」という動作が加わってきます。

「算数」における「問題文の読み取り」というものは「自分の頭で考える」ところまでもっていくことであり、それらをトータルで鍛えておく必要があるでしょう。

具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。