VOL.339【新シリーズ】中受流証明5　― ピタゴラスの定理 ―

皆さんは『ピタゴラスの定理』をご存じでしょうか。
色々ある定理の中でも知名度はトップクラスですし，直角三角形の２辺の長さがわかれば残りの１辺の長さを求めることができるので，かなり便利です。ただし，基本的に小学生では習いません。

〈図１〉

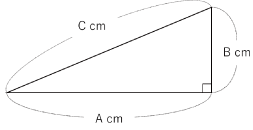
〈図１〉の直角三角形で
A^２＋B^２＝C^２
が成り立つというのがピタゴラスの定理です。
また，上の式を満たす自然数の組のことを『ピタゴラス数』といいます。
中学受験で頻出の3：4：5の（3，4，5）がピタゴラス数です。さらにピタゴラス数は無数に存在することが知られています。

今回の「中受流証明」は，《ピタゴラス数は無数に存在する》ことを証明したいと思います。

何かとんでもなく難しい気がするかもしれませんが，そのような組をいくらでも作れることがいえれば良いので，そこまでハードルが高い訳ではないと思います。
それではやっていきましょう。

〈問題〉
A^２＋B^２＝C^２…①
を満たすような自然数の組（A，B，C）が無数に存在することを証明してください。
ただし，A，B，Cには１以外に３つ全部に共通する約数はないものとします。

〈証明〉
①を変形すると
A^２＝C^２−B^２
となります。今回はこの形で証明したいと思います。

ここで舞台設定をします。
A^２…１辺がAの正方形の面積
B^２…１辺がBの正方形の面積
C^２…１辺がCの正方形の面積

C^２−B^２を図で示すと〈図２〉になります。

〈図２〉

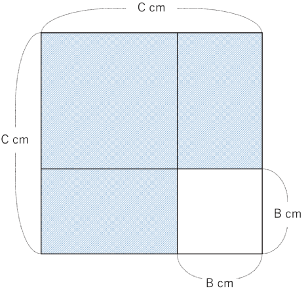
斜線部分がC^２−B^２なのでそこを１辺がAの正方形に変形することを考えます。

〈図３〉

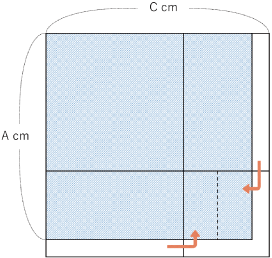
〈図３〉のように右と下の部分から長方形を切り取り，その２つの長方形の面積の合計が正方形の面積と等しくなれば目標達成となります。

ここで，〈図４〉で示すように移す方の長方形(あ)の横を１とすることにします。

〈図４〉

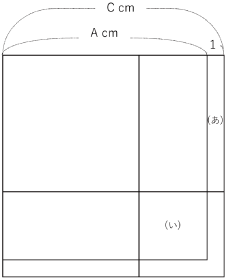
そうするとAとCの差が「１」となり，１以外の共通の約数を持たないことになります。
(あ)の縦がどういう数の時に(い)が平方数になるか考えます。

(あ)は(い)の半分なので２倍して平方数になる数が(あ)の縦です。

2×n×n（nは自然数）を縦にすると(い)は
2×2×n×n＝(2×n)×(2×n)　となり平方数となります。

〈図５〉

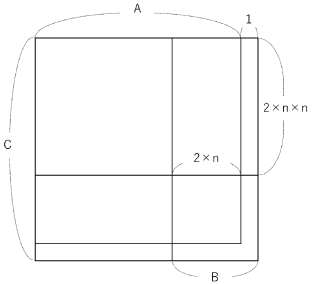
このときそれぞれの正方形の１辺の長さは以下のようになります。
A…2×n×n＋2×n
B…2×n＋1
C…2×n×n＋2×n＋1

nに1から順番に数字を入れていったときのＡ，Ｂ，Ｃがどうなるのかを以下の表にまとめました。

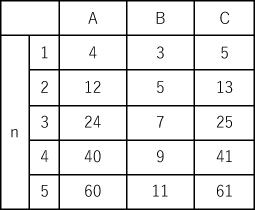
表からも明らかなようにnが決まればA，B，Cがそれぞれ決まります。自然数ｎはいくらでも存在しますから，（A，B，C）の組もいくらでもつくれます。

以上より，①を満たすような自然数の組（A，B，C）が無数に存在することが示されました。
（証明おわり）

いかがでしたでしょうか。

今回は(あ)の横が１限定でも無数にあることを示すことができました。
証明で使った面積図は全てのピタゴラス数に当てはまるので，ピタゴラス数を見つけるのに役立つかもしれません。
例えば(あ)の横が8で縦が25だと（45，28，53）というピタゴラス数があらわれます。研究するとなかなか面白いのですが，詳しいことは数学を習ってからですね。

今は中学受験に全力投球です。