VOL.110【場合の数攻略】　－フィボナッチ数列－

2019/05/17

先日、公園に行ったのですが、春らしい気候で快適な時間を過ごすことができました。
今年の春はものすごく寒い日があったという印象がありますが、それもなくなり例年のような「暑い夏」がやってくるのでしょうか。

受験生の場合、四季の変化を感じている余裕は無いかもしれませんが、今、世の中で起きていることに対して全くの無関心というのもまずい気がします。

「理科」や「社会」と関係がありそうな話題は、少し頭に入れておくとよいでしょう。
例えば「寒い春」という話題があったならば、「秋よりも春のほうが寒いことが多いのはなぜか」なんていう問に答えられるようにしておくと良いと思います。

さて、今回のテーマは「フィボナッチ数列」です。

中学受験では頻出の分野と言えますが、その内容はかなり高度です。
ですから、そんなに欲張る必要は無く、「フィボナッチ数列」であることがわかれば確実に正解できるということを当面の目標にすれば良いと思います。

まず、「フィボナッチ数列」とはどんな数列かを確認しておきます。
定義そのものは小学生が理解するのは無理だと思いますが、
結果としては
「最初の２項が０、１（（１、１）あるいは（１、２）も中学受験ではあり）であり、以後どの項もその直前の２項の和となっているような数列」
です。
具体的には
０，１，１，２，３，５，８，１３，２１，３４，５５，８９，１４４，２３３，３７７，６１０，９８７，１５９７，２５８４，４１８１，６７６５，・・・
となります。

実際は「第何項がいくつか」ということが大切なので、上記のような数列を「表」にまとめます。
直前の２項を足せばその項がいくつかを求められるので、少し練習すればほとんどの人が書けるようになります。
そうなると「第何項がいくつか」ということを悩む必要はほぼなくなりますね。

ここで、焦点が次の段階に移りました。
「その数列が「フィボナッチ数列」であることをどうやって見抜けばよいか」ということに。

そして、ここまで来て初めて「場合の数」の分野に入ってきたとも言えます。
単に「第何項がいくつか」という問題ならば、「規則性」の分野と考えられるからです。
「場合の数」の問題で「フィボナッチ数列」を使って解くものは、典型的なものが２つあります。

ひとつは「階段（１段づつか１つ飛ばし）」、
もうひとつは「長方形（１×２）の敷き詰め」です。
６年生はどちらも「基本問題」として学習済みだと思いますが、ピンとこない受験生はすぐに確認することをお勧めします。

ここまで見てきて
「フィボナッチ数列で解く場合の数（前の結果の和を利用して解くものまで範囲を広げます）」
の問題で難しいものは

「階段」「長方形の敷き詰め」ではないがフィボナッチ数列（それと見抜くのが難しい）
単に直前の二項を足した数列ではないもの

が代表例であることが分かります。

どちらにせよこれらは「学習量」でカバーできる可能性が高いです。

結果として「フィボナッチ数列」になるものは他にもたくさんあり、それらをしっかりと頭にいれておけば、かなりの「戦力アップ」となります。
少し例を挙げておきます。

最初、１辺が１ｃｍの正方形を２つ並べて長方形をつくり、以降は長方形の長いほうの辺にその辺と一辺の長さが等しい正方形をくっつけ新たな長方形を作るという操作を繰り返したときの、辺の長さ。
※これは「フィボナッチ数列」の性質のひとつである「１番目からＮ番目までの項をそれぞれ二乗（その数同士を２回掛け合わせること）したものの和は、Ｎ番目の項と（Ｎ＋１）番目の項の積に等しい」の証明になっています。
１つがいのウサギは、産まれて２か月後から毎月１つがいのウサギを産む。ウサギが死なないとしたときの、○○カ月後のつがいの数。
※これがフィボナッチさんが考案したとされる問題です。
ある整数を「偶数なら２で割り、奇数なら１を加える」という操作をその数が１になるまで繰り返す。□回の操作で１になる整数の数。

この他にも「連絡網」「白と赤の塗り分けだが赤は隣合わない」等色々あります。
経験が大切なので、沢山の問題にチャレンジしましょう。

また、全く見たこともないような問題でも、小さい数で調べたときに「５，８，１３」のような並びが出てきた場合は「フィボナッチ数列」である可能性が高いです。
そういったカンが働くようにしておくと良いでしょう。

次は「単に直前の二項を足した数列ではないもの」です。
これは「フィボナッチ数列」からは少し外れますが、考え方はほぼ同じなので、２つほど紹介します。

「トリボナッチ数列」
階段の問題で「１段ずつ」「１段飛ばし」「２段飛ばし」の３種類が可能なら「トリボナッチ数列」になります。バスケットボールの点数の入り方も同様です。
※前２つを足すのが「フィボナッチ数列」なら、前３つを足すのが「トリボナッチ数列」です。
４つは「テトラナッチ数列」だそうです。
「長方形（１×２）と正方形（２×２）の敷き詰め」
例えば２×６の長方形に敷き詰める場合は端で分類し、以下のような表に整理します。

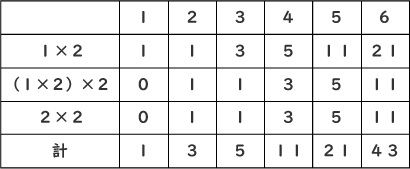
上の表を自分の力で書けるようになればこの手の問題は大抵解けるようになると思います。
大切なのは「前の結果を利用する」ということと「表に整理する」ということの２点です。