VOL.337【新シリーズ】中受流証明　― 円周率 ―

今回は中受流証明をやってみたいと思います。

昔，東大で「円周率が3.05より大きいことを証明せよ」といった問題が出題されたことがあります。
さすがに小学生の習う範囲でこれを証明するのは難しいので，一つだけ使ってよい情報を加えることにします。また，計算がかなり煩雑になるので，途中の計算は小数第三位を切り上げて小数第二位までの概数で処理する部分もあって良いことにします(この処理をしたとしても証明には支障がありません)。

それでは一緒に証明にチャレンジしましょう。

〈問題〉
１辺が8cmの正八角形の面積は309cm²であるものとします。
このことを利用して円周率が3.05よりも大きいことを証明してください。

〈証明〉
〈図１〉は正八角形に対角線を３本引きその交点をOとし，Oから辺ABに，Bから線分OCにそれぞれ垂線を引きその交点をI，Jとしたものです。

〈図１〉

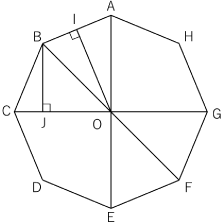
ABが8cmだとすると正八角形ABCDEFGHの面積は309cm²ですから，OIの長さは
309÷8×2÷8＝309÷32（cm）

です。また，AIは8÷2＝4（cm）ですから
AI：IO＝4：309÷32＝128：309
です。
ここで△OAIと△BCJについて考えます。お互い直角三角形で∠OAI＝∠BCJなので，２つの三角形は相似です。よって
CJ：JB＝AI：IO＝128：309＝CJ：JO

〈図２〉

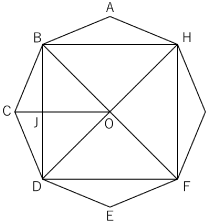
〈図２〉の△BCJと△BJOの面積比はCJ：JOに等しいので， 128：309です。さらにその比は
(正八角形ABCDEFGH－正方形BDFH)： 正方形BDFH
に等しいです。よって正方形BDFHの面積は

309×  ３０９  １２８＋３０８  ＝  ９５４８１  ４３７    (cm²)

〈図３〉

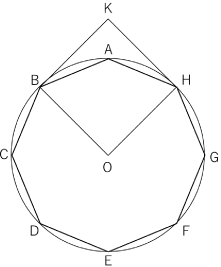
また〈図３〉の正方形KBOHの面積は，今求めた正方形BDFHの半分ですから
  ９５４８１  ４３７  ÷２＝  ９５４８１  ８７４    ･･･①

と求めることができます(単位省略)。

〈図３〉ではOを中心とする円(円O)に正八角形ABCDEFGHが内接しています。OBは円Oの半径ですから，上で求めた①は半径×半径になります。

さて，ここで大小関係について少し考えてみます。

P＞QならばP×P＞Q×Qであり，その逆も言えます。

今，円周率を3.05で計算した場合の円Oの円周と正八角形ABCDEFGHの周を直接比較する代わりに，それぞれを２回ずつかけ合わせた数値で比較することにします。

円Ｏの円周を２回かけ合わせた値
　→　直径×3.05×直径×3.05
　　＝半径×2×半径×2×3.05×3.05
　　＝  ９５４８１  ８７４   ×4×9.3025
　　≒109.25×4×9.31
　　≒4068.47･･･②

※何か所か切り上げてこの数値なので実際の円周×円周の数値はこれより小さい

正八角形ABCDEFGHの周を２回かけ合わせた値
　→　(8×8)×(8×8)＝4096･･･③

計算した結果は②＜③となりました。これは正八角形の周の方が円周よりも大きいことを示しています。実際は円周とそれに内接する正八角形の周では円周のほうが大きいのは明白なので，円周率が小さかったことになります。

以上の検討により円周率は3.05よりも大きいことが示されました。

いかがでしたでしょうか。
自力でこのような証明を思いつくことは無理だとしても，1つずつ丁寧に内容を追うことによって，理解することが出来ればそれで十分だと思います。
この証明を読んで楽しんでもらえたならば，そんなに嬉しいことはありません。