VOL.113【場合の数攻略】　－図形との融合－

よく議論されることに「中学受験は結果が全てなのか」というものがあります。
大抵の人は「結果が全てではない」と言いますし、私もそう思います。
しかし、現実にはそう簡単に割り切れるものではありません。

「努力は裏切らない」と言われるように、何かに真剣に取り組めば「良いこと」が必ずあるはずです。
その「良いこと」が「合格」ならば特に問題はないのですが、そうでなかった場合の気持ちの持っていき方が難しいのですね。

結果が不本意な場合どうしても「いくら努力しても報われない」という考え方に陥りがちですが、小学生の頭の柔らかいうちに学習した経験はそれから先の長い人生において、ずっと良い影響を与えてくれます。

ポイントは本人が「やって良かった」と気付くかどうかです。
そう、何かきっかけがあれば良いのです。

ここでよいお知らせがあります。
今「算数」に真剣に取り組んでいれば、「大学入試」で、ものすごく有利になります。そして、直接やったことがそのまま出る可能性が最も高い分野が「場合の数」なのです。

例えば、２０１７年に日本大学医学部で次のような問題が出ています。
＜問題＞

｛２，２，３，３，３，５，５｝
の７個の数字の中から６桁の整数を作るとき、６桁の整数は①通りできる。
また、そうして作った６桁の整数のうち、５の倍数になるものは②通りある。

＜答＞①２１０　②６０

実際は①の答が３桁、②が２桁ということも分かっていたので難易度は少し下がります。

解く際のポイントは「場合分け」で、
①は、
｛２，２，３，３，５，５｝｛２，３，３，３，５，５｝｛２，２，３，３，３，５｝
（後ろ２つは同じ）
をそれぞれ計算すればよく、
②は、１の位は「５」で固定なので残りの５数を
｛２，２，３，３，３｝｛２，２，３，３，５｝｛２，３，３，３，５｝
と場合分けすれば完了です。

この問題はそのまま「中学受験」で出てもおかしくありません。
中学受験経験者が「やって良かった」と思えるのはこのような問題を解いた時かもしれませんね。

何か本編のような内容になってしまいましたが、これからが本番です。
今回のテーマは「図形との融合」です。

そもそも「場合の数」は一番厄介な分野と言えます。
また「図形」に対して苦手意識がある受験生も一定数存在します。
この２つが分野の垣根を越えて一緒になると、かなり差がつきやすくなると想像することができます。

「差がつきやすい問題」は、「算数」が得意な受験生にとっては「できる側」にまわりたい問題なので、しっかりやっておかなければなりません。

※「算数」を得点源と考えていない受験生の場合、「差がつきやすい問題」よりも「皆ができる問題」の対策が重要であり、それをクリアして初めて「差がつきやすい問題」の対策をするかしないかを検討することになる。
ただし「基本」は穴がないように押さえておかなければならない。

「図形問題」の場合、「図形」を描くことが大切でしたが、これが「場合の数」となると必ずしもそうとは限らなくなります。

例えば次の問題はどうでしょう。

＜例題１＞

円周を１２等分した点があります。
この１２個の点の中から３個を選んで三角形を作るとき、全部で何個の三角形ができますか。

＜解説１＞

この問題を解くときに三角形を描いて数える人はいないと思います。
と言うか、数えたくても途中で挫折するでしょう。
実際は１２個の中から３個の点を選べば三角形が決まるので、１２個の中から３個を選ぶ組み合わせとなり
 １２×１１×１０ ３×２×１ ＝２２０（通り）　…（答）
となります。
さすがに２２０も描くのはきついですね。

あと２題、似た問題を見てみます。

＜例題２＞

＜例題１＞で、合同な三角形は同じ種類とすると、何種類の三角形ができますか。

＜解説２＞

今度は描けないこともないでしょうが、「数字への置き換え」がぴったりになります。
合計が１２になる３数の組み合わせを書き出します。
（１，１，１０）（１，２，９）（１，３，８）（１，４，７）
（１，５，６）（２，２，８）（２，３，７）（２，４，６）
（２，５，５）（３，３，６）（３，４，５）（４，４，４）
以上より
１２種類　…（答）

＜例題３＞

＜例題１＞でできた三角形のうち、二等辺三角形は何個ありますか。

＜解説＞

この問題は知らないと正解するのは難しいかもしれません。
ポイントは「正三角形」の処理です。
まず〈図１〉のように「てっぺん」を固定して二等辺三角形を描きます。
そしてそれを数えるのですが「正三角形」（点線）は抜かしておきます。
ひとつの「てっぺん」につき二等辺三角形を４個作ることができ、正三角形は全部で４個あることから、
４×１２＋４＝５２（個）　…（答）

以上見てきたように、問題によって
①「場合の数」の「公式」の利用
②数字に置き換えて「書き出し」
③部分的に図形を描き「計算」
という具合に解法が異なりました。
しかも上の解法はひとつの例であり当然他の解法も考えられます。
これは何を意味しているかというと、単に当てはめるようなパターン学習では歯が立たないということだと思います。
しかし、基本的な解法を全く知らなくても良いかというとそんなことはなく、むしろ多彩な解法パターンを「使える武器」として身につけておかなければならないと感じます。

「平面図形」と「場合の数」の融合をシンプルな問題で見てきました。
実際の入試問題はもっと複雑なことが多いでしょう。そして、難関中の難関、「立体図形」＋「場合の数」が最後の壁として立ちはだかります。

＜例題４＞

〈図２〉のように１２個の点を立方体の各辺の中点にとります。
１２個の点のうち３個以上の点を含む平面でこの立方体を切るとき、切り口として考えられる図形は何種類ありますか。
ただし合同な図形は１種類と数え、そうでないものは異なる種類とします。

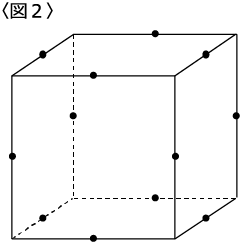
＜解説＞

この問題はかなり大変だと思います。
私が知っている問題は「何種類」ではなく「何個」かを聞いていた（答えは７５個）のでもう少し難しくなります。
①正三角形
②正方形
③長方形（１）
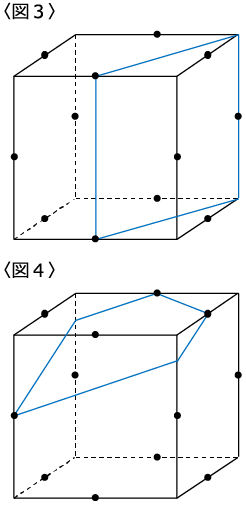
④長方形（２）･･･〈図３〉
⑤五角形　･･･〈図４〉
⑥正六角形
以上の
６種類　…（答）

ちなみに個数は
①８個　②３個　③１２個　④２４個　⑤２４個　⑥４個
です。

この問題は「作図力」、抜けがないようにする「注意力」、それと「立体感覚」が必要なのでかなりハードルが高かったと思います。
ですからできなくても悲観する必要はありませんし、正解した方は大いに自信を持ってください。

また、このような問題に試験本番で出くわしたら、とりあえず逃げることをお勧めします。
「時間に余裕がある時」のみ「正解すればラッキー」という位の気持ちで取り組んでください。
深追いは絶対にＮＧです。

「場合の数と図形の融合問題」をいくつか見てきました。

「場合の数」で特に必要だった「計算と書き出しのバランス」「言葉から違いを感じ取り解法に反映させる」、「図形」で必要だった「作図能力」「形と解法を結びつける」という両方の能力をバランス良く鍛えておかなければならないことが分かったと思います。

要求されるレベルは高いですが、ライバルに「差をつける」には絶好の機会ですから、前向きに頑張っていきましょう。

具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。