VOL.105【図形に強くなる】 -正確な作図(2)-
先日ゴルフの打ちっ放しで練習をしました。
インターネットで動画を観ていたら、ある有名なティーチングプロが面白いことを言っていたのでそれを確かめたくなったのです。
所謂セオリーと言われるものがあり、アマチュアの皆さんはその通りにやろうとしますがなかなかうまくいかないそうです。
そこで、そのプロの先生は逆のことをやるようにアドバイスをすると、生徒がナイスショットを連発し、自分でも信じられないといった表情をしているのです。
私も動画でプロが言っていたいくつかの言葉を頭に入れ、それ以外はほとんど何も考えずにボールを打ってみました。
不思議なことにほぼ動画通りの結果になり、それまで全く当たらなかったドライバーがかなりの確率で当たるようになったのです。
これは何を意味しているかというと、「セオリーというものは大抵トップレベルのプレイヤーを基準に確立したものであり、一般的なプレイヤーには必ずしも当てはまらない。
それぞれのレベルに合ったアドバイスが必要であり、「言葉」によるイメージによって結果をガラリと変えることができる。」ということだと思います。
とても良い勉強になりました。この経験を生徒の指導に活かしたいと思います。
さて、「立体図形」の攻略に移りましょう。
今回は「平面図形」でもやった「正確な作図」です。
今回も「方眼ノート」に描くことを前提に進めていきますので、よかったらお手元に「方眼ノート」を用意して実際に描きながら読み進めてもらえばと思います。
- 見取り図
「立方体」
「立方体」の見取り図は描く機会も多く皆さん慣れているとは思いますが念のため解説しておきます。
正面にくる面を正方形にすればそれなりの見取り図にはなるでしょう。
お勧めの描く順番があるので、以下の図で確認して下さい。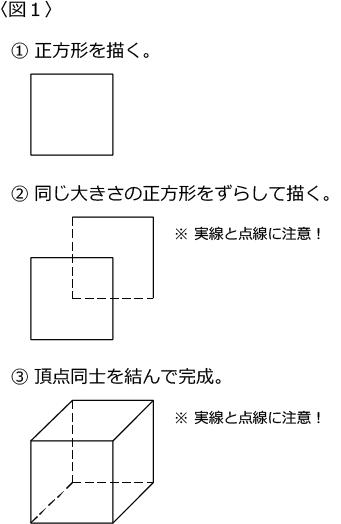
「四角すい」
底面が長方形(正三角形も含む)である四角すいを扱うことが多いですが、その底面は「見取り図」では「平行四辺形」になります。
その「平行四辺形」の4つの頂点を「四角すい」のてっぺんの頂点と結んであげれば出来上がりです。
〈図2〉はかなり丁寧に作図しています。
てっぺんの頂点を決めるところは、少し簡略化してもかまいません。
自分なりの作図法を見つけてください。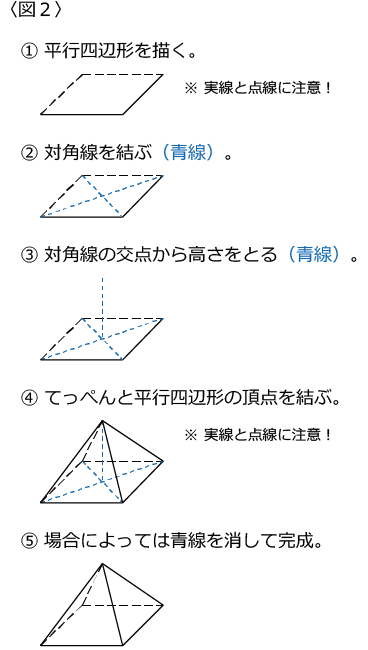
- 「立体切断」に必要な作図
〈図3〉は1辺が12cmの「立方体」です。
以下の3点を通る平面で切断した時に必要な作図について考えてみます。
i)A、B、P
ii)A、B、Q
iii)A、B、R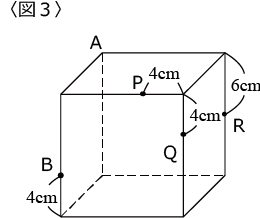
i)いきなり見取り図に書き込んで十分でしょう。〈図4〉
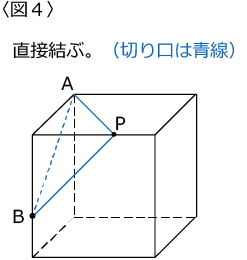
ii)結べるところは結んでから投影図を利用しましょう。
手順は〈図5〉を参考にしてください。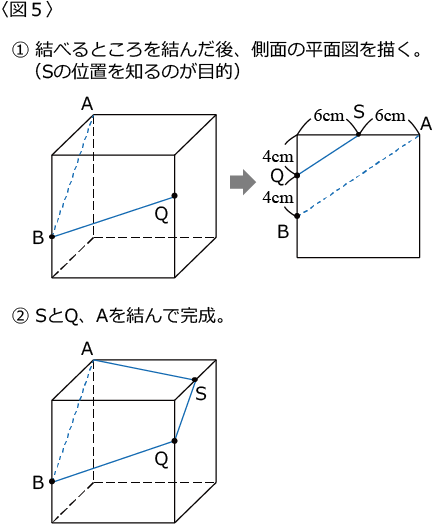
iii)今回のメインです。じっくり取り組んでください。
〈図6〉にかなり詳しいものを載せておきました。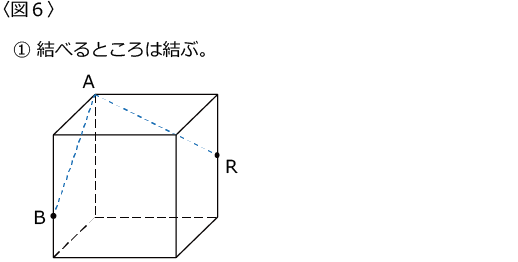
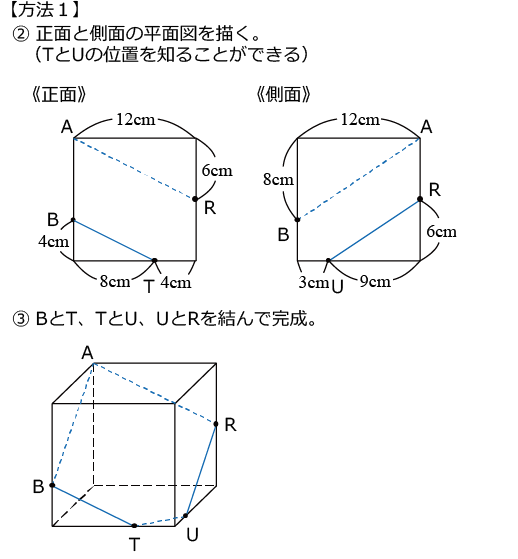
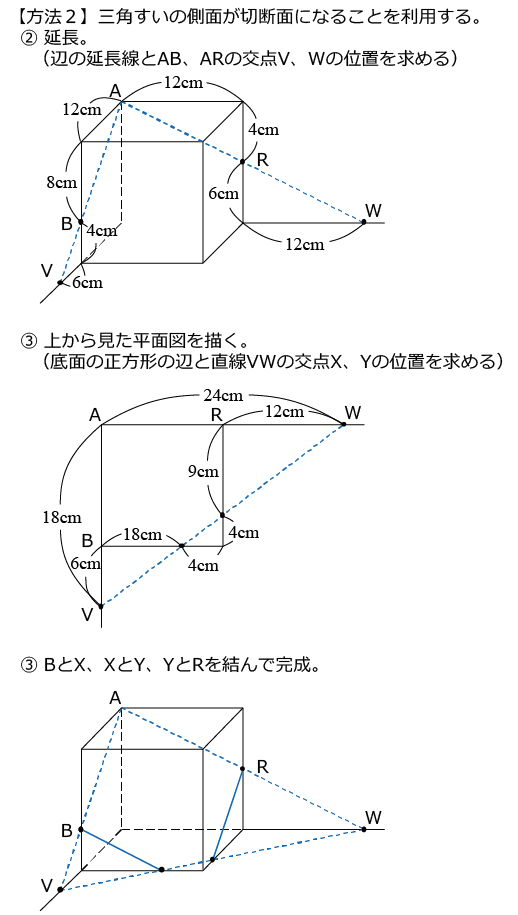
これで「立体切断」の作図で困るようなことはあまりないと思います。
Vol.57の今週の1題の解説でも、かなり詳しく作図法を解説してありますので参考にしてください。
また、これらの方法を知っているだけでは対応が難しそうな問題もVol.28の今週の1題に用意してありますので、目を通しておくことをお勧めします。
「作図」は本人が描かなければ身につきませんので、今回の内容を踏まえ、しっかり練習してください。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★★★☆
〈図1〉の四角すいO-ABCDは底面が正方形で、側面の4つの三角形は全て合同です。
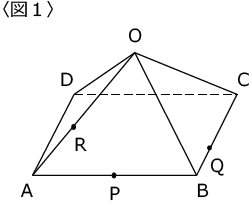
点P、Q、Rはそれぞれ辺上にあり、
AP:PB=1:1
BQ:QC=1:2
OR:RA=3:2
です。
3点P、Q、Rを通る平面で、この四角すいを切断するとき、以下の問に答えてください。
(1)切断面と辺ODとの交点をS、辺OCとの交点をTとするとき、OS:SDとOT:TCをそれぞれ求めてください。
(2)2つに分かれた立体のうち大きい方の立体の体積は四角すいO-ABCDの体積の何倍ですか。
分数で答えてください。
解答が表示されます













