VOL.104【図形に強くなる】 -なぜ「立体図形」は難しい?-
前回「補助線」について説明しました。
基本的に「補助線」というのは、その場で自分で編み出すような類のものではなく、決まった形から欠けているものを埋めてあげるようなイメージの方がうまくいきます。
また、ほぼ損をしない線というものも存在し、それを引いて問題を眺めれば、かなりの確率で正解にたどり着けると思います。
いずれにせよ「図形」の場合も知識の土台がしっかりしていないといけませんが、その際「形」と結びつけておく必要があり、その点が「数量」の問題との違いになっています。
今シリーズのタイトルは【図形に強くなる】ですが、実は少し後悔しています。
このタイトルだと「立体図形」を避けて通れないからです。
私個人にとって「立体図形」は得意分野です。
そして、指導した生徒のほとんどが「立体図形」を得意分野にすることに成功しています。
私は、人間にはまわりの人間をコピーする能力が元々備わっていると考えています。
ですから、生徒に「立体図形」をできるようになってもらう方法として、「私の頭の中をコピーしてもらうこと」を少し意識しています。
※実はこれが「教える」ということの本質かもしれません。
昔から、「人から直接教わることが何かを習得する際の最も効率が良い方法である」と考えられています。
ところが、Web上では私の頭の中をコピーしてもらうことはさすがに不可能でしょうから、別の方法でいかなければなりません。
ということで、まずは「なぜ立体図形は難しいのか」を考えてみたいと思います。
そもそも「立体図形」の問題のほとんどが、小学生が習う範囲を超えていると考えられます。
入試問題に「すい体の体積を求める公式」が添えてある学校があることからもそれがわかります。
もっとも、中学受験に範囲はあってないようなもの、センター試験と同等なレベルの問題が出題されることもザラです。
ということは、塾等で習う範囲というのは過去問の蓄積により確立されたものであり、必ずしも基礎から積み上げられたものではないということです。
そうなるとどうしても理論の飛躍や、結論だけを示されるケースもでてくるでしょう。
中学受験は時間との闘いでとにかく忙しいですから、これは仕様がないことかもしれません。
しかし、受験生によっては何かしっくりこなかったり、よくわからないので算数が嫌いになってしまったりと不都合が生じます。
このような受験生の目には、「立体図形」は何か得体のしれないものに映っていることでしょう。
具体例を挙げます。
中学で習う「数学」では「空間図形」という括りになりますが、最初に「定義」から入り、「点」「直線」「面」の関係性をかなり詳しくやります。
例えば2本の「直線」の位置関係は
- 重なる
- 1点で交わる
- 平行
- ねじれ
が考えられます。
そして
「立方体ABCD-EFGHの各辺のうち辺ABとねじれの位置にある辺を全て答えよ」
といった問題で練習するわけです。
また2つの「平面」の位置関係は
- 重なる
- 交わる
- 平行
が考えられます。
2つの「平面」が交わるときその交わりは「直線」になりそれを「交線」と呼びますが、このことが理解できていないと近年出題が増えている「立体を複数の面で切断する問題」に対応することができません。
私の経験では、塾で最上位クラスに在籍していた受験生もこの「交線」についての理解が不十分なことが多かったように思います。
「基本を徹底する」ことの難しさのあらわれですね。
ここまでで私が言いたいことをまとめると以下のようになります。
- 「立体図形」は「柱体の体積や表面積を求める問題」以外はそもそも小学生が扱うには少しハードルが高い分野かもしれない。
- とは言え実際には各校でかなりの難問まで出題されている。
- 塾は「出題されたものは解けるように対策を講じなければならない」と考えるのが普通。
- 解けるようにはしてあるがその元になる土台の部分まできちんと指導しているかどうかは不明。
- 結果(担当した生徒の様子)から推測するに、基本の徹底は難しいのが現状であると思われる。
このように考えると「立体図形」を難しく感じている受験生が多数いることも納得できます。
それでは対策に移りましょう。
今までの話から明らかなように、「基本の徹底」につきます。
ではどうやって「基本」を身に着けるかですが、「人から直接教わる」しかないように思います。
それはなぜかというと「空間認識能力」は個人差が大きいからです。
算数は積み重ねの学問ですから、一つずつ本当にわかっているかどうかを確認しながら次のステップに進まないと大ケガをします。
これが集団授業だと一旦わからなくなってしまうと二度と追いつけない可能性すらあります。
では自分のペースで参考書を使って学習するのはどうでしょうか。
これが「計算」のようなやれば確実にできるようになる分野ならまだしも、「立体図形」の独学は無謀というものです。
参考書や問題集の解答には正解に至るまでの考え方は書いてあるでしょうが、一番肝心なその「立体」を本人が認識可能になるまでのプロセスが書かれていません。
当たり前ですが、この部分の個人差が大きすぎるので書物にすることはまず無理なのです。
奇跡的にその本の著者と感覚がほぼ一致していて、解説を読むだけで全て自分のものにできるという受験生もいるかもしれませんが、そういったことは稀でしょう。
ただブログの発信者としては、結論が「指導者から教わってください」というわけにはいかないので、次回からできることはやっていきたいと思います。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★★☆☆
名門君は「円」の面積の公式がなぜそうなるのかを調べてみました。
色々な説明がありましたが、その中でも「おうぎ形に分割して互い違いに並べ、平行四辺形に近い形を作る」というやり方がわかりやすいと思いました。※<図1>参照。
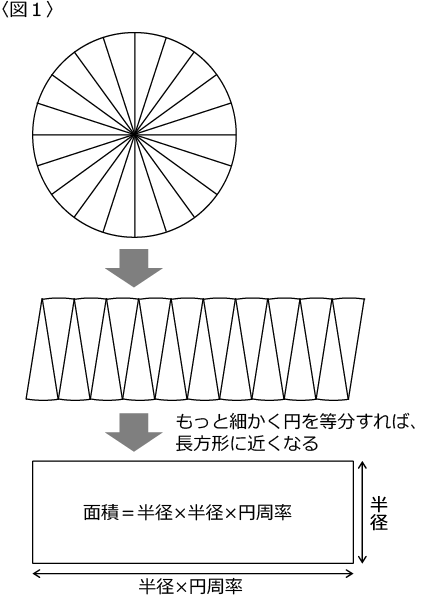
また、底面積と高さが等しい「すい体」は、どれも体積が等しいということも本を読んで知りました。
名門君はこのことから「球」の表面積がわかれば、体積が計算で求められると考えました。
そして、「球」の表面積は、底面の半径が球の半径と等しく、高さが球の直径と等しい「円柱」の側面積と同じであることを、お隣のお兄さんから教えてもらいました。
それを元に、自分の考え方で半径6cmの「球」の体積を計算したところ、900cm3になり、名門君の考え方が正しかったことがわかりました。

(1)名門君は半径6cmの「球」の表面積を求める際、円周率を3.14ではなく、ある分数で計算していました。
その分数(仮分数でかまいません)を求めてください。
(2)〈図2〉のように半径が6cmの「球」を8等分しました。
1つあたりの表面積を求めてください。
ただし円周率は3.14とします。
解答が表示されます













