VOL.106【図形に強くなる】　－立方体－

先日船に乗る機会があったのですが、とても楽しい時を過ごすことができました。
ただ、子供のころは船に乗るのは苦手だった思います。

原因は船酔いです。
元々、車でも酔ってしまう体質だったので、船はきつかったはずです（なぜか、記憶はほとんどありませんが）。

どうやって克服したかというと、単純に慣れたのです。
学生の時、ひと夏の間、屋形船に乗るアルバイトをしたのですが、最初の２、３日の地獄を抜けたあとは、何も感じなくなりました。

このことは「算数」にも当てはまるような気がします。

• 「苦手克服」はまず慣れること。
• 最初はきついかもしれないが、それを抜ければどうってことはない。
• 一度「克服」してしまえば、その後は同じことで悩む可能性は低い。

「算数」の場合は３日では「苦手克服」は難しいでしょうが、抜けた先には楽しい世界が広がります。
一緒に頑張っていきましょう。

さて、今回のテーマは「立方体」です。

代表的なものを解説していきます。

i）展開図

「立方体」の「展開図」は全部で１１種類です。
まず、この「１１」は何となく頭に入れておくとよいでしょう。
そして、大切なのは、自分なりに「展開図」の形を分類し、その気になれば１１種類全部を描けるようにしておくことだと思います。
〈図１〉が１１種類の「展開図」です。
私なりの分類をしておきました。
おすすめです。

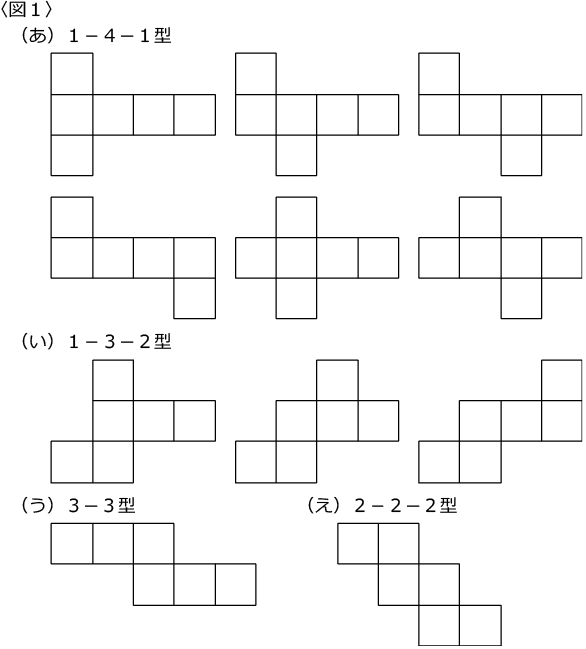
また、有名な「立方体の最も遠い頂点同士は、展開図上では二つの面をつないでできた長方形の対角にくる」というのも使い勝手が良いです。
〈図２〉を参照してください。

ii）立方体のくりぬき

ズバリ「輪切り方式」が有効です。
複雑な問題になると頭の中だけで処理するのは相当大変です。
なので、段ごとに書き出す「輪切り方式」が良いのですね。
特に「体積」を求めるときに有効で、ほぼ数えるだけの問題にすることができます。
「表面積」を求める問題の場合は「輪切り方式」よりも「投影図」が有効ということもあります。

≪問題≫
〈図３〉のように、４×４×４＝６４（個）の１辺１ｃｍの小立方体で作った立方体があります。

これを〈図４〉のように３方向から反対側まで小立方体を取り除いた立体の、体積と表面積をそれぞれ求めてください。

≪答≫　体積…４７ｃｍ^３　　表面積…１３６ｃｍ^２

〈輪切り方式〉

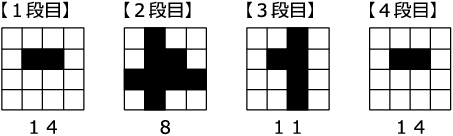
１４+８+１１+１４＝４７（ｃｍ^３）

〈投影図〉

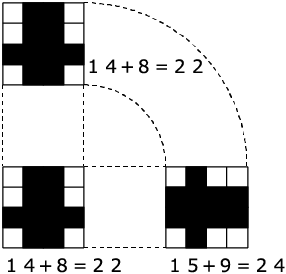
（２２+２２+２４）×２＝１３６（ｃｍ^２）

iii）立方体の積み木

私はよく「数量→図形」という変換を行うと良いと言っているのですが、この「立方体の積み木」の場合は「図形→数量」が有効です。
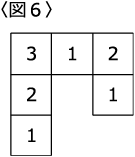
〈図５〉のような立体は〈図６〉のように上からみた時、何段重なっているかを数字で書きます。
これで「体積」も「表面積」も対応できます。

以上のようにそれぞれ有効なやり方がある程度決まっているので、勉強はしやすいと思います。慣れるまでチャレンジを続けましょう！

具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。