VOL.308入試本番に高得点を取るための冬休みの過ごし方
今回は冬休みの過ごし方について書きます。
冬休みはまとまった時間が取れるので、学習が大いに進むでしょう。
肝心なのは、かけた時間が点数に変わるような学習を心がけることだと思います。
4教科受験の場合、特に大切なのは4科目のバランスです。
苦手科目を作らないということが肝心です。
4教科全てで受験者平均点程度を取ることを目標とし、得意科目で少し上乗せして合格を掴むという戦略が効率の良いものです。
逆に言えば、得意科目でドカンと稼ぐような戦略は危険と言えるでしょう。
苦手科目は1科目が限界で2科目苦手なら即アウトに近いです。
もちろん個々の事情等あるでしょうから、全員がバランス型とはいかないでしょう。
個々の実情に合わせた戦略を練らなければならないのは当然です。
ただ、冬休みを4教科のバランス調整期間に充てるという考え方が最もリスクが少ないのではと考えています。
算数と国語は短時間で得点を伸ばすのは難しいと言われています。
逆に理科と社会の知識で解決する部分は覚えてしまえばすぐにでも点数アップが見込めます。
と言うことは、理科社会が仕上がっていないのならば、冬休みには理科社会を重点的に強化するのが効率的であると考えられます。
実はこの時のために算数の実力アップにじっくりと取り組んできたとも言えます。
本ブログの読者ならば、算数の実力はすでに十分なレベルに到達しており、後は本番に向けてきっちりと調整するという状態になっていると思います。
ということで、冬休み以降のお勧めの調整法を書きたいと思います。
※まだまだ実力が足りない、という受験生については次回書きます。
①テスト形式
テスト形式で問題を解く場合は以前書いた「戦略」を意識して解くようにしてください。
これをやることによってかなりの得点アップが見込めます。
以下にリンクを貼っておきます。
VOL.301 VOL.302
分野・難易度がアトランダムであることが肝心で、全体的な難易度が志望校の難易度に対し易しいものか、同等なものがお勧めとなります。
易しいものの効果は「自信をつける」「基本の確認」が考えられ、同等なものの効果は「予行演習」「合否判定」に使えることが考えられます。
難しいものはあまりお勧めしていないのですが、私の授業では使うようにしています。
効果は「限界突破」「思考力の養成」といったものがあり、上手くいけば大きな効果が期待できます。
ただし、デメリットもあります。
「結果的に時間の無駄」「自信喪失」「知識の混乱」等が考えられるので、私は授業内だけに限定して使っています。
特にお勧めなのは易しいもので、出来れば毎日取り組んで欲しいと思います。
週に1回か2回適正な難易度で行えば十分でしょう。
私がつくる予想問題のようなものは出来が良かったことが多いです。
特に、似たような問題が本番で出題された時は結果も上々です。
今後も質の高いものを提供したいと思います。
②基本の反復
基本はどこまでいっても大切なのは明白でしょう。
少し前の「単元別学習」に書いたやり方がそのまま使えます。
VOL.304を参照してください。
問題は何をやるのかということです。
今までやってきたものを継続することが考えられますが、正答率が90%以上ならば切り替えの必要もあるでしょう。
冬休みが切り替えのラストチャンスで、それよりも後になってしまうと、中途半端になる恐れがあります。
新たに取り組むものは正答率が60~70%の「基本書」が良いと思いますが、受験本番までに最低でも4回は繰り返すことができる見通しが必要です。
間に合いそうもない場合は、今までやってきたものを繰り返すのがお勧めです。
その際、タイムアタックをすると良いでしょう。
驚くほどタイムが短縮されると思いますよ。
また、「基本書」の繰り返しはやっていなかったという受験生は「今すぐ」始めてください。
今から始めればまだ間に合います。
最優先事項ですね。
③過去問
①と同じような効果があるのですが、それを過去問で行うということです。
第一志望を10年分やるのは常識のようになっています。
中には何回も繰り返せ、と言っている人もいますが…
個人的には1回に集中すべきだと考えています。
①との違いは「1度出題された問題と同じものはもう出題されない」ということです。
「予想的中」といった効果は期待できないということですね。
そうすると、過去問を繰り返しやることはデメリットが多く、得策ではないということになります。
ただ、①で使うテストを自分で探したり作ったりといったことは指導者がいないと厳しいので、古い過去問を活用することは大いに考えられます。
また、学校によっては20回、30回とやった方が良いと思われる学校もあります。
トップ3は
・麻布
・筑波大附属駒場
・灘1日目
でしょうか。
そういった細かい事情は指導者に相談するのが一番だと思います。
何年(回)分やるかはかなり重要です。
また、過去問の直しもネックになる可能性があります。
過去問の解説は今までやってきたことと無関係であることがほとんどなので、学習の流れが遮断されてしまうのです。
ここでも指導者がいると大きなメリットとなります。
「この問題は以前やった問題集のこの考え方が使えるよ」というアドバイスがどれだけ貴重なものか、イメージしてみてください。
冬休み以降のおすすめの調整方法を3つ紹介しました。
これ以外にも色々あるでしょうが、私は以上の3つを家庭学習としてもらい、授業で補完するというやり方をすることが多いです。
結果は良好なので、皆さんにもお勧めする次第です。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★★☆
〈図1〉は1辺が6cmの正方形ABCDに2本の対角線を引き、その交点をEとしたものです。
さらに正方形ABCDの外に点Fをとり、AとF、BとF、DとFを結ぶと∠AFDが45°になりました。
AFとDCの交点をG、ACとBFの交点をHとするとき以下の問いに答えてください。
〈図1〉

〈図2〉
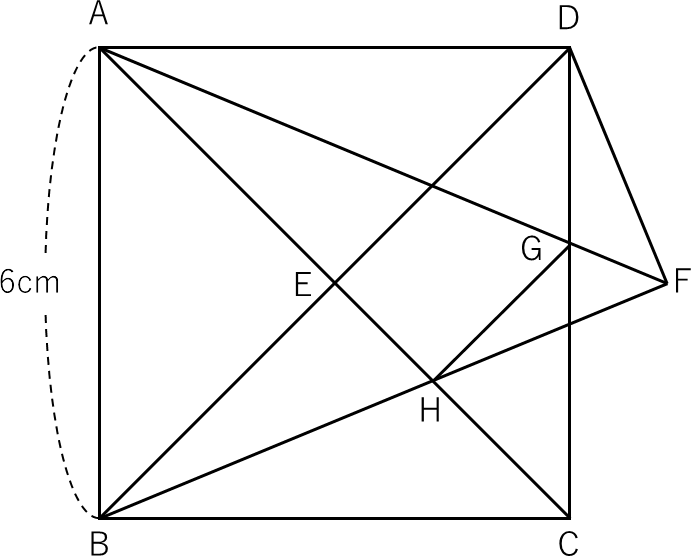
(1)∠AHGは何度ですか。
(2)AHを1辺とする正方形とHCを1辺とする正方形の面積比が3:1だとすると、三角形BFDの面積は何cm2ですか。
解答が表示されます













