VOL.3251問全力解析 2024年度 市川中学校
今回の1問全力解析は2024年市川(帰国)5です。
まずは問題を見てください。
まずは基本テーマから見ていきましょう。
基本テーマ
①立体の切断
②単純にするための工夫
③立体版ツノ出し
④作図・平面図の利用
⑤体積比
この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。
①立体の切断
苦手にしている受験生が多いテーマです。
分かってしまえば簡単ともいえるので,立体の切断の出題があった学校を受ける場合はしっかりと対策をしておきたいところです。
まずは立方体の切断を,切り口の図形ごとに理解することが肝心です。
②単純にするための工夫
本問は直方体2個を組み合わせた立体に対しての斜め切断でそれなりにハ-ドルが上がっています。
そのままでも解けますが,必要な部分に絞り,割りっ切って答を出すことも可能でした。
そのためには,両方の直方体を含む立方体の切断のイメージを持てると良かったと思います。煩雑さがかなり解消されました。
③立体版ツノ出し
平面図形では必須の技術である「ツノ出し」ですが,立体でも重宝します。
立方体の切断で切り口が五角形になるようなケースで,三角すいを付け足すことで直方体の斜め切断で切り口が平行四辺形になるものとみなすことができます。
④作図・平面図の利用
立体の切断では切り口がどうなるのかがはっきりするような作図を行う必要があります。
本ブログでかなり丁寧に手順を説明してあるので参照してください。VOL.105
本問の場合,平面図によるアシストがあるとより分かりやすくなるので,のちほどやってみたいと思います。
⑤ (1)は体積を求める問題ですが,体積比を使いたいところです。
三角すい台は,全体と切り取った部分が相似になるので,「切り取った部分と全体の相似比が分かれば体積比もわかる」ということを前提に,どこの数値を求めれば良いかを明確にしながら解き進めるとよいでしょう。大幅な効率アップが見込めますよ。
以上を踏まえて問題を解いてみましょう。
〈解説〉
(1) まずは正方形TUVWを1つの面とし,Aを1つの頂点とするような立方体Pをイメージします。
立方体P
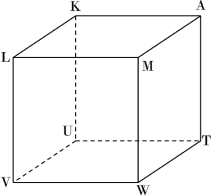
続いてAIとKUの交点をN,AJとMWの交点をOとし,その平面図を描きKNとMOの長さを求めます。
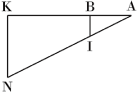
BI= 1 2 cm,AB=1cm,AK=3cmより
KN= 1 2 ×3=1.5(cm)
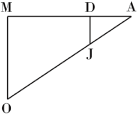
DJ= 2 3 cm,AD=1cm,AM=3cmより
MO= 2 3 ×3=2(cm)
この時点で切り口となるANとAOを描き,LVを延長し「ツノ出し」を行い,作図を完成させます。
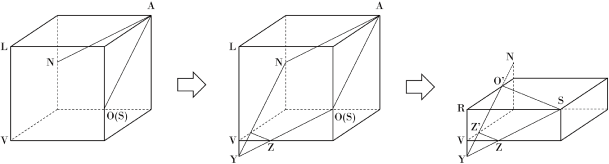
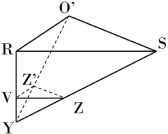
YV=1.5-1=0.5(cm)
VZ=3× 1 3 =1(cm)
VZ’=3× 1 4 = 3 4 (cm)
「ツノ出し」をした三角すいと全体の相似比は1:3なので,体積比は
1×1×1:3×3×3=1:27
求める三角すい台の体積はツノ出しした三角すいの
27-1=26(倍)
よって,
1× 3 4 × 1 2 × 1 2 × 1 3 × 3×3×3-1 1×1×1 =1 5 8 (cm)・・・(答)
(2) Iの位置は(1)と同じなので,Nの位置も同じです。立方体に対して3点ANJを通る平面で切断します。
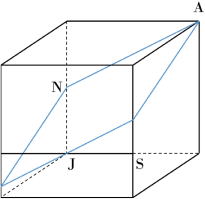
ANとJを通る切り口は平行です。
平面図を描くと下のようになります。
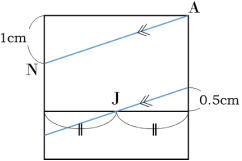
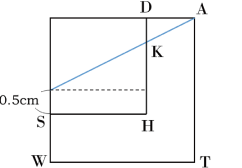
求めるDKの長さは,
3 2 × 1 1+2 =0.5(cm)・・・(答)
いかがでしたでしょうか。
帰国生向けの問題でしたが,一般と変わらない印象を受けました。
本問の完答が合格に必要だったかどうかはわかりませんが,正解できればその分有利になったのは間違いありません。
算数だけで考えるとするならば,帰国といえども一般と変わらない対策を行う必要があるように感じました。
大変かもしれませんが頑張っていきましょう。
名門会ブログでも,市川学園の帰国生入試と学校の様子をご紹介しています。以下のリンクからご覧になれますので,是非ご参考になさってください。
「市川中学校・高等学校」
中学・高等学校の先生に聞く! 中学受験帰国生入試レポート
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。