VOL.3261問全力解析 2024年度 暁星中学校
今回の1問全力解析は2024年暁星4です。
まずは問題を見てください。
まずは基本テーマから見ていきましょう。
基本テーマ
①群数列
②グループ番号
③三角数
④約分できるとは
⑤見当をつける
この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。
①群数列
分数列の場合,分母で分類し1つの塊にすると規則性が見えてくることが多いです。
本問の場合も同じ分母を一塊とみれば,分子は1から順番に1つずつ大きくなっています。
このように,数字を各群に分けられるような数列を「群数列」と呼んでいます。
②グループ番号
群数列であると見抜き,仕切り線を入れたならば,先頭からグループ番号を1から順に振りましょう。
そして,各群の中身とグループ番号の関連を調べます。
本問の場合,グループ番号をNとすると
・グループの数字の個数 → N×2
・グループ内の分数の分母 → N×2+1
この2つを押さえておくとよいでしょう。
③三角数
Nグループまでの個数は「三角数」の2倍になっていることを確認してください。
三角数を求める公式は
(1+N)×N÷2
ですが, Nグループまでの個数はその2倍なので
(1+N)×N
求められることになります。
④約分できるとは
約分できる分数の個数を数えるのはそんなにやさしくありません。
約数の個数というわけではないので,注意が必要です。
素因数分解を利用すると計算の上だけで数を求められますが,書き出してしまうのが実践的だったようにも思います。
後で両方やってみます。
⑤見当をつける
③で公式化しておいたことがここで活きます。
ただ,ピッタリその数になるわけではないので,おおよその見当がつけばよいことになります。
45×45=2025
なので,45グループまで調べれば良いと見当をつけておきます。
さらに, 6 13 を 42 91 を約分したもの(これが一番最後なので求める分数は 30 65 ではないかと予想できれば…
また,(1)の答を考えると一番最後の分数の分母は91なのではないかと見当をつけることもできます。
すこし際どいところもありますが,スンナリと答が出ると思います。
以上を踏まえて問題を解いてみましょう。
〈解説〉
(1)分母が87は
(87-1)÷2=43
より〔43グループ〕だとわかります。〔42グループ〕までの総数は
(1+42)×42=1806
なので,〔43グループ〕の前から82番目は
1806+82=1888(番目)・・・(答)
(2)分母が素数でなければ約分ができます。素数ではない奇数を小さいものから順番に調べていきます。
| 分母 | 約分できる分数の分子 | 個数(個) | 式で解くやり方 |
| 9 | 3,6 | 2 | 9=3×3 → 3-1=2(個) |
| 15 | 3,5,6,9,10,12 | 6 | 15=3×5 → (5-1)+(3-1)=6(個) |
| 21 | 3,6,7,9,12,14,15,18 | 8 | 21=3×7 → (7-1)+(3-1)=8(個) |
| 25 | 5,10,15,20 | 4 | 25=5×5 →5-1=4(個) |
最後の 20 25 でちょうど20個ですから
(答) 20 25
(3)45×45=2025
なので,〔44グループ〕までの総数を求めてみます。
(1+44)×44=1980(子)
よって〔45グループ〕の44番目までが範囲とわかります。
また,〔45グループ〕の分母は
45×2+1=91
なので,
6 13 = 42 91
より求める分数の1つ後ろは 42 91 となり,その1つ前は分母が奇数であることを考慮すれば 30 65 であることが分かります。
分母65は
(65-1)÷2=32(グループ)
です。〔31グループ〕までの総数は
(1+31)×31=992(個)
なので,求める答は
992+30=1022(番目)・・・(答)
いかがでしたでしょうか。
しっかり差がつく問題に仕上がっていたと思います。
次の5整数の性質(約数の個数,総和)に関する問題 もそうですが,知識の充実が必要な問題ともとれるので,対策によって結果が変わった可能性が大きかったのではないでしょうか。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題規則性
難易度★★☆☆☆
〈図1〉のような正三角形のタイルがあります。これと同じ大きさのタイルをすき間なく並べ〈図2〉のような大きな正三角形をつくります。そして,〔1段目〕のタイルに1,〔2段目〕のタイルに左端から順に3,4,5,〔3段目〕のタイルに左端から順に5,6,7,8,9,〔4段目〕のタイルに左端から順に7,8,9,10,11,12,13と番号をつけます。このあとも同じ規則で〔50段目〕まで番号をつけていくとき,以下の問いに答えてください。
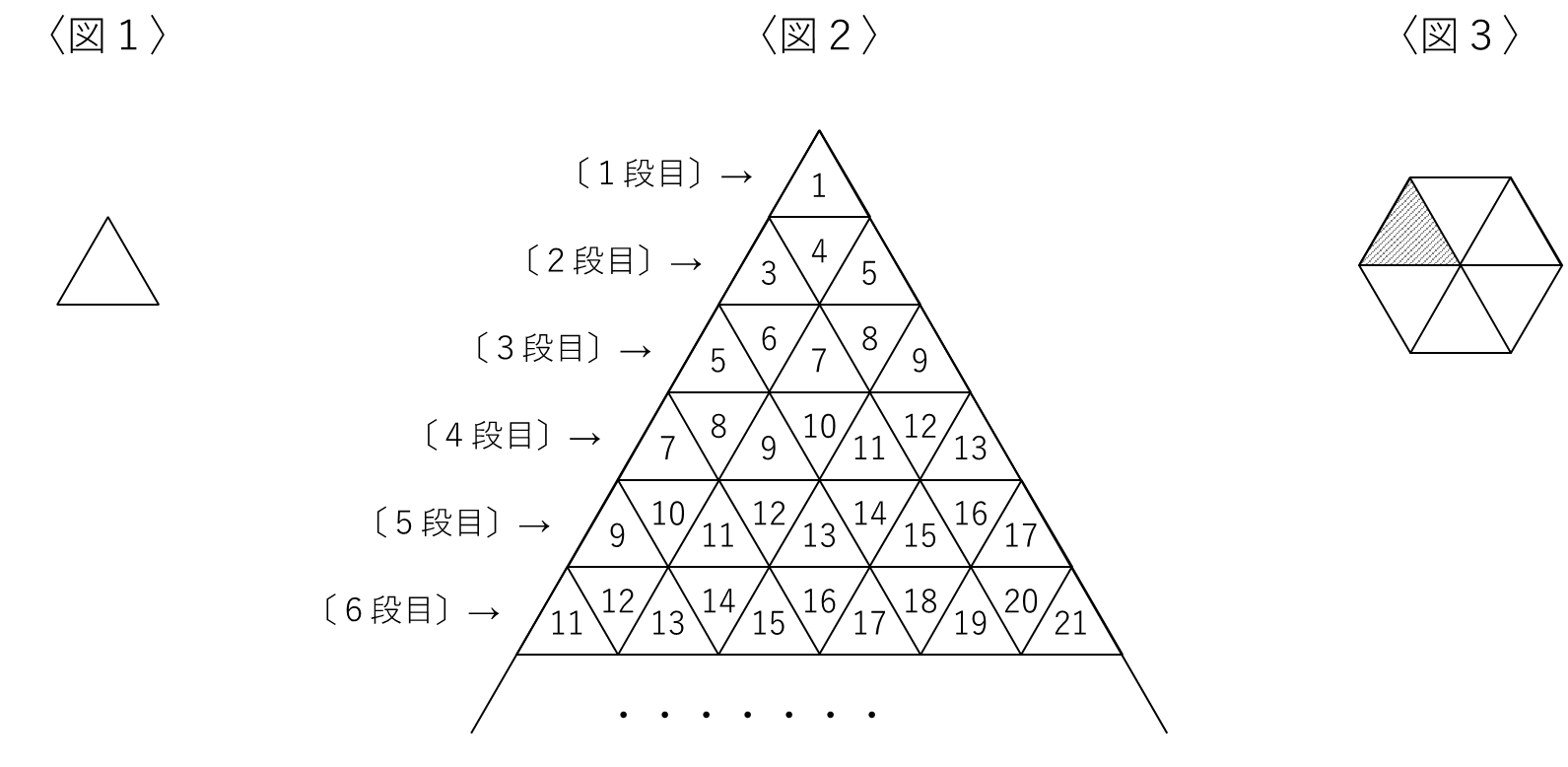
(1)〔50段目〕についている数字の和を求めてください。
(2)〈図3〉のような正六角形になる6つのタイルについている数字の合計が501になるとき,〈図3〉の斜線部の正三角形についている数字はいくつですか。
また,そのようになる正六角形はいくつありますか。
解答が表示されます














