VOL.3211問全力解析 2024年度 女子学院中学校
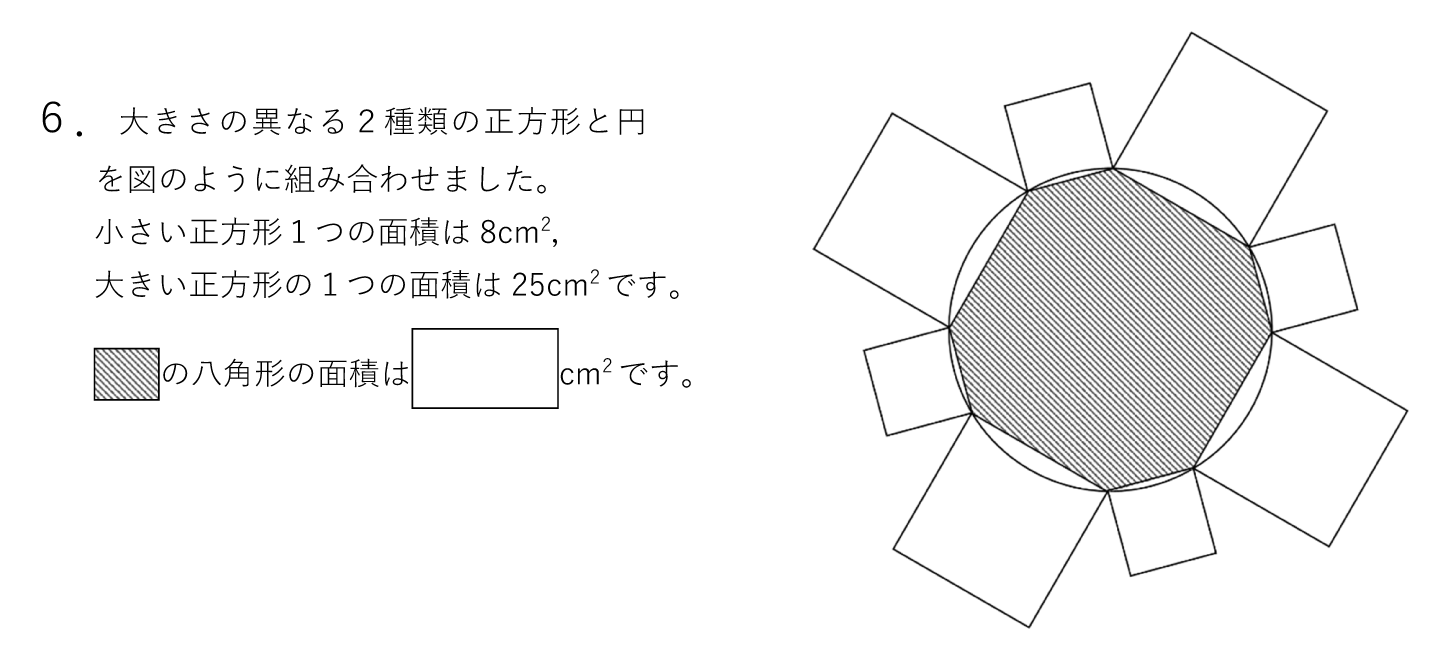
今回の1問全力解析は2024年 女子学院6です。
まずは問題を見てください。
基本テーマ
①八角形の分割
②組み合わせて整形
③何がわかれば良いかの把握→図形から数量
④平方根(√)は理解している方が有利か
⑤図形にこだわってみる
この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。
①八角形の分割
正八角形では当たり前の9個に分割する補助線が本問でも有効です。
※正八角形の分割についてはVOL.206の今週の1題の解説を参考にしてください。
正方形1個、合同な直角二等辺三角形4個、合同な長方形4個に分割されました。
②組み合わせて整形
実は上の分割法は2つあり、どちらでも結果は同じです。見やすいのは真ん中の正方形が小さくなる方で、その面積は問題文の小さい正方形と同じです。
直角二等辺三角形は2つ組み合わせても4つ組み合わせても正方形をつくることが出来ますが、本問では4つ組み合わせます。
そしてそれは問題文の大きい正方形と同じです。
③何がわかれば良いかの把握→図形から数量
最後に残ったのは長方形ですが、この長方形は縦も横も小学生が習わない数値になっているので、何か工夫が必要です。
長方形の面積は縦×横なのでそれさえわかれば良いと把握することが肝心しょう。
本問の場合縦×縦と横×横はそれぞれ求めることができるので、その積はどうなるのか、といった発想で解くことが可能です。
ただ、それまでは図形のパズル感覚だったものが、数量(2次方程式)に変わるので目的意識がハッキリしていないと諦めてしまった可能性があったと思います。
④平方根(√)は理解している方が有利か
一定数の受験生が平方根を利用して解いた可能性があります。必要な計算は
5√2 2 ×2√2=10
です。これ以外にも1辺が5の正方形の対角線が5√2のような計算も求められます。
結局、これらの計算の理解にどれだけの時間をかける必要があり、その完成度はどうなのか、といった問題があり悩ましいところです。
ただ、理科の振り子のように2乗に比例する場合は平方根が出てきてしまうこともあるので、平方根の理解にチャレンジすることは悪くないと思いますし、実際本問も最後は簡単な2次方程式になっています。
余裕があれば、平方根を学ぶこともよいのではないでしょうか。
⑤図形にこだわってみる
私は日頃「図形>数量」を説いています。
これは図形的処理を数量的処理よりも優先すべし、ということなのですが、本問は半々の感じでした。
実は小学生が扱う範囲の図形的処理でも答がでるので、後ほど紹介したいと思います。
何かないか、自分で色々と考えてみることは「力」をつけるには良いことなので参考にしてみてください。
以上を踏まえて問題を解いてみましょう。
〈解説〉
〈図1〉のように補助線を引きます。
〈図1〉
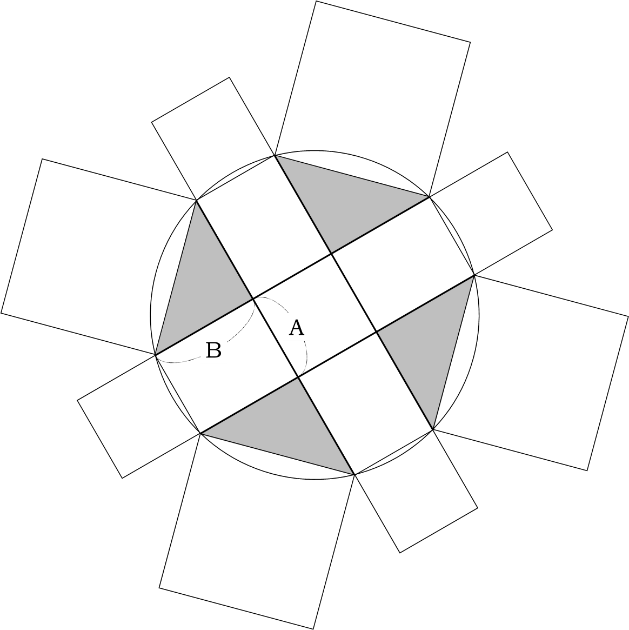
八角形を9分割しました。
真ん中の正方形の面積は小さい正方形と同じなので8cm2です。
4つの直角二等辺三角形は4つくっつけて正方形にすると大きい正方形と同じになるので25cm2と求められます。
長方形は縦(短い方)も横も今のところ不明ですから、ここを解決することが必要になります。
ここで長方形の縦をAcm,横をBcmとおきます。
A×Aは小さい正方形の面積なので8(cm2)です。
また、B×Bは直角二等辺三角形2個分なので25÷2=12.5(cm2)です。
よって以下の式が成り立ちます。
(A×A)×(B×B)=8×12.5
=100
=10×10
よってA×Bは10です。
これらをまとめて
8+25+10×4=73(cm2)・・・(答)
◎長方形の面積を求める別解
〈図2〉のように2つの辺がAの直角二等辺三角形と2つの辺がBの直角二等辺三角形をまわりが正方形になるように並べます。
〈図2〉
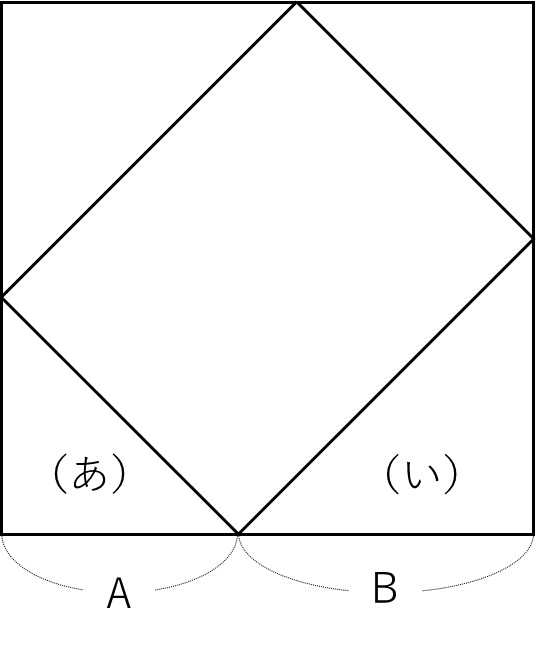
図の(あ)2個分の面積は小さい正方形に等しいので8cm2です。また(い)2個分の面積は大きい正方形の面積の半分なので12.5cm2です。
また、(あ)の斜辺を1辺とする正方形の面積は小さい正方形の2倍ですから16cm2となります。よって(あ)の斜辺は4cm、同様にして(い)の斜辺は5cmであることがわかります。
以上より〈図2〉の正方形の面積は 8+12.5+4×5=40.5(cm2)
となります。
次に〈図2〉と同じ正方形を〈図3〉のように分割します。
〈図3〉
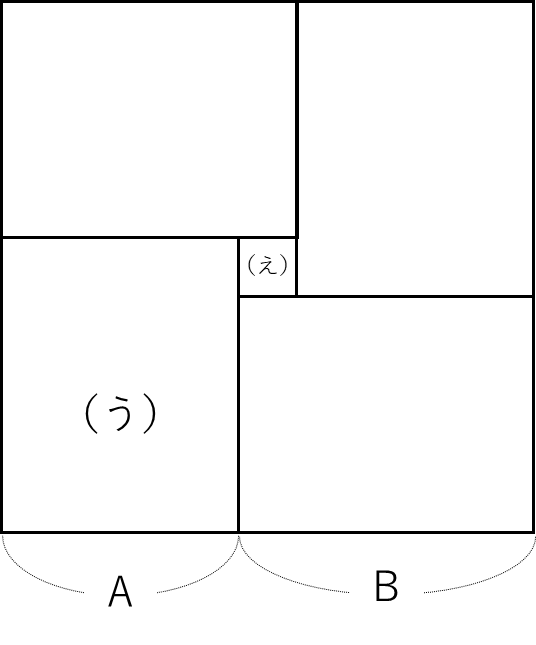
図の(う)の面積が求める面積です。
〈図2〉の直角二等辺三角形の斜辺が4:5だったことよりA:B=4:5
図の(え)の1辺は正方形の1辺の
9-4×2 4+5 = 1 9
です。よってその面積は
40.5× 1 9 × 1 9 =0.5(cm2)
以上より求める長方形の面積は (40.5-0.5)÷4=10(cm2)・・・(答)
いかがでしたでしょうか。
かなり平方根的な感覚が必要な問題だったので、苦労した受験生もそれなりにいたと思います。
このような問題が増えてくると「平方根もやっておかなければ」という発想も浮かんでくるかもしれません。
私はどちらかというと、その発想には反対で、むしろ別解で示したような考え方を鍛えられればと考えています。
平方根についてはVOL.240で取り上げているので参照してください。
余裕があれば平方根を身につけるのは大いに結構ですが、無理はしないことをお勧めします。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。