VOL.322１問全力解析　2024年度　武蔵中学校

今回の１問全力解析は2024年武蔵４です。
まずは問題を見てください。

基本テーマ
①最初が肝心
②全体の把握
③出題者の意図を汲み取る
④前の結果の利用→表にまとめる
⑤対称性・余事象

この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。

①最初が肝心
(1)はA=3のときの1点ですから，やさしい問題と言えます。
ただ，舐めてかかりそこで間違えてしまうと，全滅が待っています。
最初の問題だからこそ，慎重に，確実に正解を手繰り寄せましょう。
(1)の場合，全部書いたとしても6通りですから，その全ての点数を調べれば正解したも同然です。

②全体の把握
(2)が意外と厄介だったかもしれません。
これも全部書けば24通りで，そのほとんどが1点と2点です。
本問は(4)が主眼なので，誘導になってはいるのですが，それは(3)あってのことなのです。
正解者の大半は全部書いたと思われますが，(3) (4)に少しでも目を通していれば違った解き方になったかもしれません。

③出題者の意図を汲み取る
(3)は(2)よりも明らかにやさしいです。5個書いて調べれば良いだけですから。
普通は違和感を感じるはずですが，出題者の意図を想像するとなかなか面白かったりします。
これはあくまで私の想像ですが，出題者は次のように考えていたのではないでしょうか。
「A＝3やA＝4なら書けば答が出るよね。でもA＝6ならどうですか？720個は書きたくないよね。実はうまい考え方があるんだけど，君たちは気付くかな？」

(3)の重要性に気付いて欲しいところです。

④前の結果の利用→表にまとめる
Aが3，4，6と増えていくような場合，前の結果を利用する可能性が高いです。

本問も「いかにも」なのですが，この手の問題の中では比較的複雑になっていました。なので，（3）でしっかりと把握しておくことが重要だったのですね。

前の結果を利用する場合は，表にまとめるのが常套手段ですが，本問はその点でも厄介でした。
どうまとめたら良いか分からなかった受験生も相当数いたことでしょう。
後ほど私のまとめ方を見ていただきます。

⑤対称性・余事象
(2)から，出題者の意図はA＝5を求めそれを使って(4)の答をまともに出すルートであると考えられます。
もちろんそれで何も問題はないのですが，何か他に無いのかと考えてしまうのが我々の習性です。
有力なのが対称性と余事象の利用です。
こちらも後ほど見ていただくことにしましょう。

以上を踏まえて問題を解いてみます。

〈解説〉

(1)　全部書きます。

１２３ 1＜2，2＜3　2点

１３２ 1＜3，3＞2　1点

２１３ 2＞1，1＜3　1点

２３１ 2＜3，3＞1　1点

３１２ 3＞1，1＜2　1点

３２１ 3＞2，2＞1　0点

以上より，
4通り…（答）

(3)　異例ではありますが，(2)は後回しにして(3)からやっていきます。

これも全部書きます。

ⅰ）５１３２４ → 2点

ⅱ）１５３２４ → 2点

ⅲ）１３５２４ → 3点

ⅳ）１３２５４ → 2点

ⅴ）１３２４５ →3点

（答）2点，3点

ここで点数の増え方をまとめておきます。

㋐ Aが1増えると，前に比べて点数は「＋0点」か「＋1点」になる。

㋑ 一番大きい数が左端に入ると「＋0点」

㋒ 上の〔１，３〕の並びのように１点が入っている所の間に１番大きい数が入ると１点増えるかわりにすでに入っていた１点がなくなってしまうので，「＋０点」

㋓　㋑，㋒のケース以外は「＋１点」
例えば既に２点になっているところに一番大きな数を入れる場合，「＋０点」は左端(ⅰ)と点数が入っている所(ⅱ)(ⅳ)の間なので，３通りとなります。
Aを入れられる場所が全部で（A＋1）通りなので，「＋１点」は，そこから上の3通りを引いて（A−2）通りとなります。

(2) (4)
(3)の考察を踏まえ表にまとめます。最終的に2点なので途中考えられる点数は０，１，２点です。

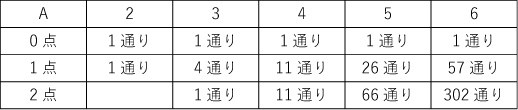
※・０点はどこも１通り
・０点→１点　は，A－1（通り）
・１点→１点　は，前の通り×2（通り）
・１点→２点　は，前の通り×(A−2)（通り）
・２点→２点　は，前の通り×3（通り）

表より(2)１点…11通り，2点･･･11通り
(4)302通り

〈(4)の別解〉
対称性を考慮すると，A＝6の時は０点と５点，１点と４点，２点と３点が同じ通りあることがわかります。
６個の数字の並びは
6×5×4×3×2×1＝720（通り）

なので，１点，２点，３点の合計は360通りであることがわかります。

よって表を使えば
360－(1＋57)＝302（通り）･･･（答）

と求めることができます。
実際はA＝4のところまでは(2)を解いてわかっているのでA＝5の１点を
4＋11×2＝26（通り）
と求め，さらにA=6の1点を
5＋26×2＝57（通り）
とやれば答に到達します。

現実的には正攻法で答を出し，確かめで別解を使えばスマートだったと思います。

いかがでしたでしょうか。

本校の場合，何年か前から点数を取らせてくれるような設問があるように感じます。

本問も実は大サービスだったわけですが，本来ならば(4)を正解できなければいけないと金田は思うのです。
普段の学習の際は，同じ設定でAが大きいときの２点や３点が出せる位に鍛えて欲しいです。
出題した先生もきっと正解して欲しかったはずです。

その期待に応えられるよう頑張っていきましょう。