VOL.3201問全力解析 2024年度 開智中学校
今回の1問全力解析は2024年開智(第1回)4です。
まずは問題を見てください。
まずは基本テーマから見ていきましょう。
基本テーマ
①書き出し
②ヒントで確認
③大きく捉える
④3の倍数の性質
⑤計算でいきたい
この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。
①書き出し
(1)では15番目と30番目が問われています。十分書き出せる範囲でしょう。
本問の場合はここでの書き出しで全体像を掴みたいところです。
②ヒントで確認
親切にも20番目が282と教えてくれています。さすがに15番目と30番目は正解できるのではないでしょうか。
大切なのは、変な勘違い等がないことを早めに確認することでしょう。
③大きく捉える
本問の場合、結果的には全て書き出して数えるという戦略でもいけました。
ただし、「勉強」という観点で言えばこの問題は計算でも解けるようにしておきたいところです。
2024までではなく、10000以下といった設定も考えられますから・・・。
計算で求めるには全体像を捉える必要があります。
そうなると、桁数で分類して、それぞれを計算することになるでしょう。
④3の倍数の性質
3の倍数は「各位の和が3の倍数」になります。
そうすると上の③で考えた、桁で分類するという考え方との相性が良いことに気づきます。
2+2=4までは決まっていますから、残りは2,5,8・・・ ですね。
⑤書き出しと計算のバランス
本問のように書き出しでも計算でもいけそうな場合、少し悩ましいかもしれません。
普段の学習から、書き出しと計算のバランスを整えておき、場合によってはどちらかで答を出しておき、もう一方で確かめる、といった戦略をとれるようにしておきたいところです。
私は基本的にはまずある程度書き出して、その後計算でいける見通しが立てば極力計算で答を出すようにしています。
バランスには個人差があるので「100個までなら書き出す」「はっきりした規則性が見つかるまで書き出し」といった戦略が得策ということもあるでしょう。
大切なのは自分なりのスタイルを確立しておくことです。
以上を踏まえて問題を解いてみましょう。
〈解説〉
全部書き出すと以下になります。
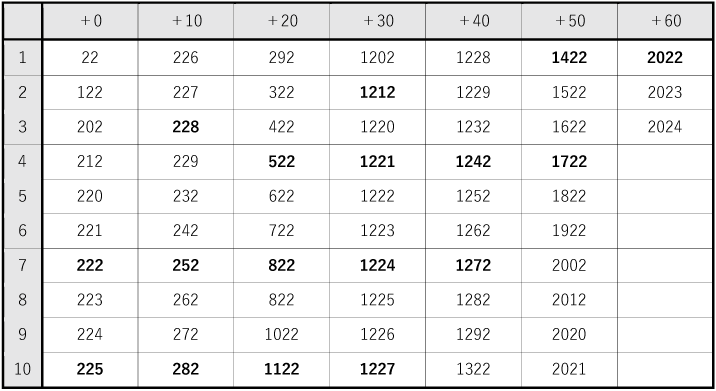
(1) 上の表より
(答) 15番目・・・232
30番目・・・1122
(2) 上の表より
(答)63番目
(3) 上の表中の太字のものが3の倍数なので
(答)17個
(4) 上の表より
(答)1、36回
〈別解〉
(1) 222(7番目)の次からは1の位が3~9まで1つずつ増えていきます。よって229は
7+9-3+1=14(番目)
次は232なので
(答)15番目 232
292は282(20番目)の次なので21番目。その次は322で、以下百の位が4,5,6・・・9と1つずつ増えていきます。
よって922は
21+9-3+1=28(番目)
* 3桁までは2以外の数(9個)に関しては全て3個あり、(2,2,2)は1個なので
9×3+1=28(個)
あることが確かめられました。
そこから先は1番目から28番目までの数に千の位の1を加えた数になるので、
29番目→1022
30番目→1122・・・(答)
(2) 1922は 28×2=56(番目)
2000以降は下2桁に2が1個以上あればよいので
(0,2)→ 2個
(1,2)→ 2個
(2,2)→ 1個
(2,3)→ 1個
(2,4)→ 1個 計7個
以上より 56+7=63(番目)
(3) 3数ないし4数の組み合わせからそれぞれ何個あるか調べます。
(2,2,2) → 1個
(2,2,5) → 3個
(2,2,8) → 3個
(1,1,2,2)→ 3個
(1,2,2,4)→ 3個
(1,2,2,7)→ 3個
(0,2,2,2)→ 1個 計17個・・・(答)
(4) 1000台が28個あるので、1が2番目に多いのは明白です。
1~28番目までの1および3~9は全て3回ずつです。
2000台の1は2012と2021の2回なので
3×2+28+2=36(回)
(答)1、36回
いかがでしたでしょうか。
両方のやり方で確かめながら答を出すのは少し贅沢過ぎるとは思います。
局面に応じ、計算を重視するかどうかの選択でしょうが、結局は全部書いたかどうかで解き方が決まったような気がします。
入試本番は恐怖があるでしょうから、全部書き出した受験生が多かったとは思いますが、正しく書き出せるという保証はありません。ですから、計算とのすり合わせは必要だったのではないでしょうか。
規則性は正解することが全てとも言えるので、本問のような良質な問題でしっかりと練習しましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
長さがAmmのパイ生地をこねることを考えます。
図の手順でパイ生地を 1 3 に折り曲げて重ね3倍に伸ばすことを,パイ生地を1回〔こねる〕とします。点P,Qはパイ生地の上にあり,パイ生地を1回こねると図のように点Pは点Qに移動します。

たとえばA=90,χ=70のときy=60です。
(1) A=90とします。〔1回こねる〕とPはQに移動します。このときのχとyの関係を表すグラフを下の図に書き込んでください。
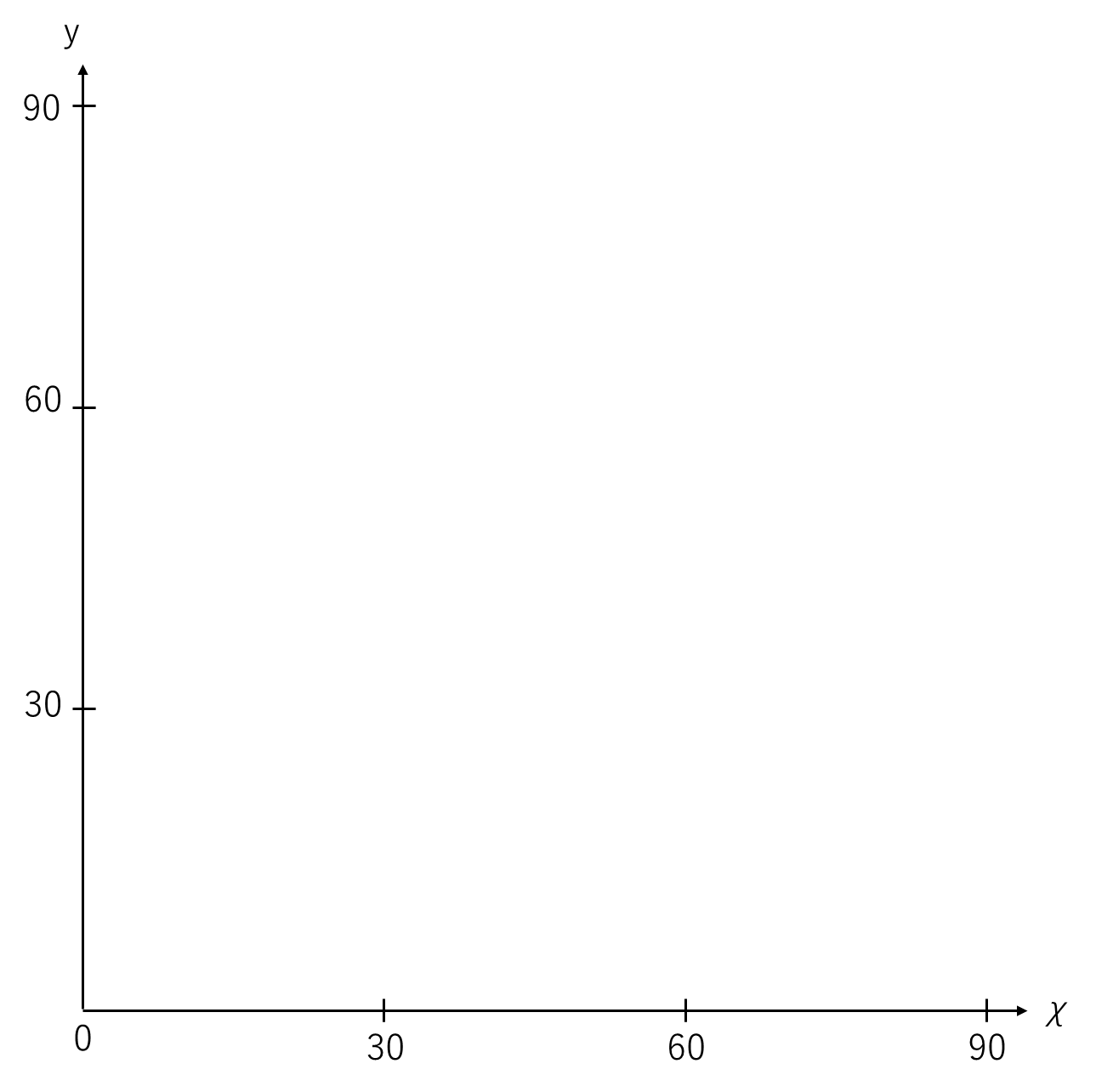
(2) 〔こねる〕ことを2回続けて行ったとき、yはχの半分になったといいます。このようなPとして考えられる点はいくつありますか。ただし、χ=0はのぞきます。 また、考えられるχが全て整数となるような最小のAはいくつですか
解答が表示されます