VOL.302試験中の戦略2
前回の続きです。
「半分の時間で半分正解し、残りの時間で残りの半分を正解する」というのが、合格に必要な点数をキープする基本戦略でした。
もちろん、その時の難易度等で必要な点数は変わってきますから、どれ位の点数を狙うかという方針決定を含めて、前半の時間を有効に使う必要があります。
もう一つ重要なのは、まずは全体に目を通すということです。
分野の確認はチラッと見るだけでも可能なので、最初にすることをお勧めします。
さて今回は、半分の時間で半分の正解が確保出来た後について考えます。
もう少し厳密に言うと、全体に目を通した上で比較的得点しやすい問題から手を付けて、一段落ついた状態です。
ここまでにかかった時間が制限時間の半分程度で、正解をキープしたのがおよそ半分を目指しましょうという話です。
後は残りの時間をいかに有効に点数に変えていくかということなので、今回はその話になります。
残っている問題には既に濃淡がついています。
1わからない
2わかりそうだが解けていない
3解けそうだが解いていない
4解けるはずだが敢えて飛ばした
5評価せず飛ばした
以上が考えられます。
通常は3と4のところに力を入れ、正解をキープすれば目標達成の可能性が高いです。
「過去問演習」や「模試」で優先的に練習すべきなのが、3や4を正解に持っていくことだと思います。
ここがきちんとできるようになれば、試験本番での失敗はほぼ無くなるでしょう。
時間に余裕がある場合や3と4だけでは点数が足りない場合についても考えてみます。
時間に余裕がある場合は「確かめ」を最優先にしましょう。
それが終わった後は時間さえかければ正解できそうな問題に取り組むのが良いと思います。
また、そもそも評価していない問題は簡単に解ける可能性もあるのでチェックは忘れないようにしましょう。
3と4だけでは足りないと思われる場合は状況判断が大切になってきます。
リスクを承知で点数を取りにいくのか、安全策を取るのか。
このあたりの判断の練習も「過去問」「模試」で意識しておきましょう。
5はチェックするとして、2を正解に持っていけるかどうか、ここが勝負所です。
私の授業のイメージはこのギリギリの状況で正解できる「力」を育むイメージで行っています。
普段の学習はここで正解側に回れるだけの「力」の養成を目指してください。
因みに1はどうするかということもあると思います。
突然わからないものがわかるということもありますから最後まで諦めないということも大切ですが、現実的にはできればラッキーという姿勢がよいでしょう。
「深追いしない」、これだけは忘れないでください。
分野で考えた時、「立体」と「場合の数」の二大難所は考え方を変えるべきでしょう。
「立体」は本人が得意か苦手かで変わります。
得意なら積極的に解き、苦手ならば消極、場合によっては手をつけないのが良いでしょう。
「場合の数」は難易度で変わります。
典型問題(順列や組み合わせの公式で解けるような問題)はむしろ得点しやすいので積極的に解き、そうでない場合はとりあえず保留です。
最後まで保留するか、書き出して数えるか、なんとか計算で求めるかはその場の判断です。
複雑な問題は勝算が立ちにくいので、正解すればラッキーという場面以外では逃げることをお勧めします。
最後に、今までの戦略がそもそも使いにくいケースについて説明します。
大問4~6題で小問が少ないようなケースでは半分の時間で半分という単純なことにはなりにくいかもしれません。
このような場合は、どの分野から解くのかを事前に決めておくのが得策になるでしょう。
例えば大問5問で①「数の性質」②「場合の数」③「速さ」④「平面図形」⑤「立体図形」と並んでいた場合、私なら④⑤①③②の順番で解くと一応決めています。
とにかく自分の得意な分野から解くという姿勢が大切です。
おいしいものから食べるイメージです。
大問4~6で構成される学校の場合は1題あたりにかけられる時間を事前に決めておき、それをオーバーしないように解き進めるようにしてください。
この練習も「過去問」がメインになります。
例えば開成の場合、大問4問だったならば1問にかけられる時間は計算上
60÷4=15(分)
ですが、少し余裕をみて12分程度に設定しましょう。
4題に手をつけるのにかかる時間は
12×4=48(分)
以内ですから、まだ12分以上余る計算になります。
そこで仕上げをどうするか判断するという流れになるでしょう。
学校によって考え方を変える必要はあるかもしれませんが、前半の早い段階でなるべく多く点数を確保するという姿勢は変わりません。
後半は「時間」を有効に「点数」に変えるという意識で、得点の最大化を目指してください。
残りの期間はこのことを意識して「過去問」「模試」に取り組み、算数の「力」を最大まで伸ばせるよう頑張ってください。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★★★☆
〈図1〉の四角すいOABCDは底面が正方形で側面が全て二等辺三角形です。
〈図1〉
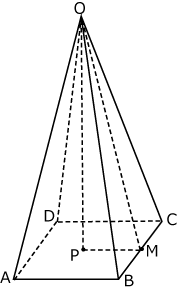
また、底面の正方形の対角線の交点をP、辺BCの中点をMとすると、
PM:MO=1:4
です。
OPが15cmのとき、以下の問いに答えてください。
(1)四角すいOABCDに内接する球(5つの面全てと接する球)の半径を求めてください。
(2)四角すいOABCDの体積を求めてください。
解答が表示されます













