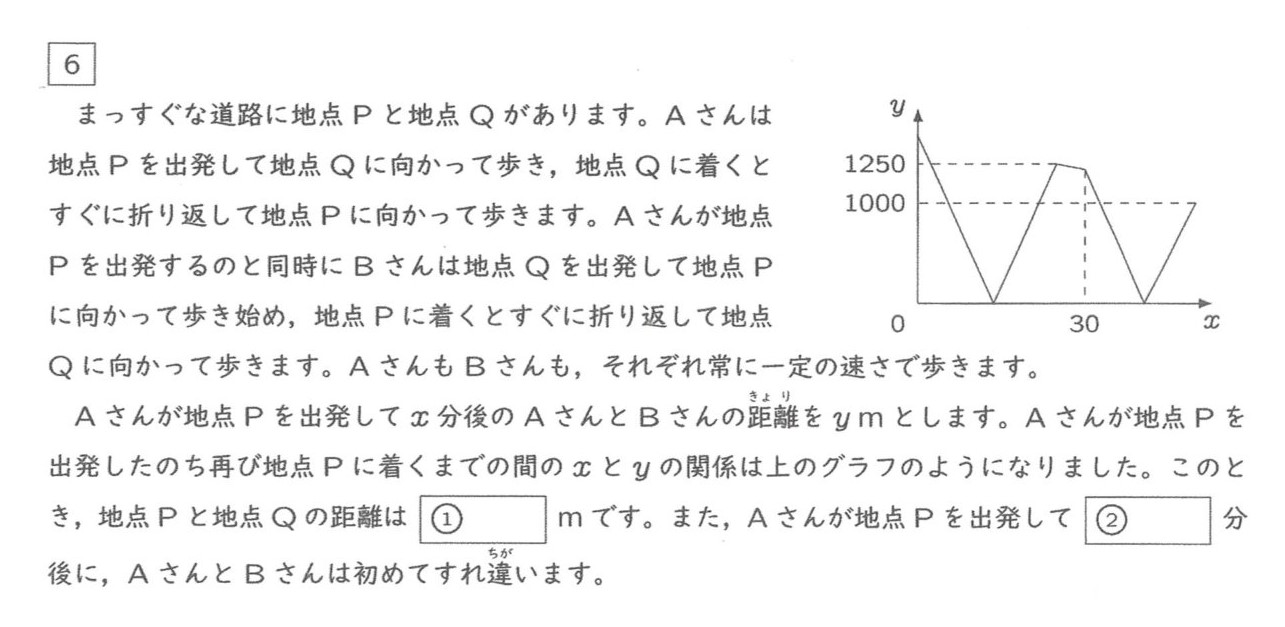
VOL.276１問全力解析　2023灘中学校

今回の１問全力解析は２０２３年灘１日目６です。
まずは問題を見てください。

この問題では以上のような基本テーマが潜んでいると考えられます。
ひとつずつ見ていきます。

①問題文を良く読む
速さの問題ですが、よくある二人の差のグラフが与えられるタイプです。
このグラフは折れ方が複雑になることが多く、苦手とする受験生も一定数いると考えられます。
慣れてしまえばさほど難しくないことがほとんどで、本問も本校の合格レベルの受験生は難なく正解したことでしょう。
ただし、ひとつひとつ丁寧に読み取っていかないと何がおきているのかが見えてこなかったと思われます。
その意味では読解力が要求された問題だったと言えるでしょう。

②節目に何があったのか ～ストーリーを紡ぐ
このタイプのグラフが出てきたら、グラフが折れた所で何が起きたのかを考えなければなりません。
また、ｙの値が「０」になった時は２人は同じ場所にいるので、それも大きなヒントになります。
・同時にスタート
・出会う
・１人目（速い方）が到着、すぐ折り返し
・２人目も到着
・２回目の出会い　
・速い方が戻る（グラフ終わり）

※終わった状況からＡが速いことがわかります。
この流れが見抜ければ大丈夫でしょう。

③グラフをおこす
２人の位置関係がわかるようなグラフを描くのが良いでしょう。
スペースがあれば元のグラフの真下に、横軸が揃うように描けば正確なものを描くことができます。
この後の解説で具体的な手順を説明します。　　

④比の利用
本問はヒントとなる数字が少なめです。
「時間の情報」が１つ、「距離の情報」が２つです。
「距離」の２つの数字を比に置き換えると、それだけでかなり前進することになります。
コツは、「距離」の比と同じ比になっている「時間」を探すことです。
それを見つける時に使うのが③で取り上げたグラフで、比を書込みやすいのもグラフのメリットです。
次の⑤も含め、全部がつながってきました！

⑤グラフは図形
グラフは描いてしまえば図形として見る姿勢が大切です。
特に三角形の相似がほぼ現れるので、活用しましょう。
本問も最後の仕上げは「砂時計型」の相似を利用します。

※旅人算は使わなくてもよければ（他の解法を思いつけば）、使わないことを推奨します。
これについてはＶＯＬ．１１７に詳しく書いたので参照してください。

以上見てきたように、差のグラフの問題は位置のグラフを起こせれば解けたも同然と言えます。
以上を踏まえて問題を解いてみましょう。

グラフを描きます。
その前提として押さえておくべきことをメモしておきます。
・同時スタートからＡさんが往復して戻ってくるまでがグラフとして与えられている
・Ａさんが往復を終えたときＢさんはＰから１０００ｍの所にいる→Ａさんの方が速い
・Ｂさんが片道にかかる時間は３０分
・速さは一定なので直線のグラフになる（片道）
〈図１〉

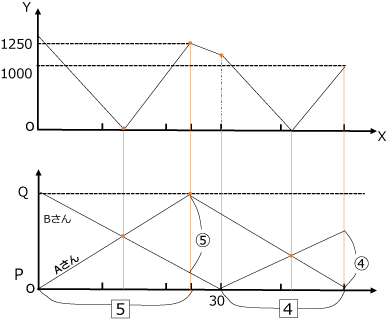
１２５０:１０００=５:４
なので、５:４になっている時間を探します。
→グラフに記入
ここまで準備できればもう大丈夫です。
ＡさんとＢさんの片道にかかる時間の比は
５:５×２
４=５:６
なので速さの比は逆比で６:５です。
よってＰＱ間の距離は
１２５０÷５×６=１５００（ｍ）…①の答
初めてすれ違うのにかかる時間は砂時計型の相似を使って
３０×  ５  １１  =１３  ７  １１  （分）…②の答
きれいに解決しました。

以上見てきたように隔たりのグラフの問題はそんなに恐れる必要はないと思います。
しっかり考えれば解けるという自信さえ持てれば、解けたも同然ですよ！