VOL.275１問全力解析　2023桜蔭中学校

今回の１問全力解析は２０２３年桜蔭中Ⅳです。
まずは問題を見てください。

この問題では以上のような基本テーマが潜んでいると考えられます。
ひとつずつ見ていきます。

①読解力
本問は最近の流行とも言える長文です。
最後の問題であり、立体に移動がからんでいますから最初から引き気味になってしまった受験生もいたかもしれません。
実際はそこまで難しくなく、できれば完答したい問題でした。

ただし、単純な立体図形の問題ではなく移動の要素があるので、そこは注意が必要です。
その移動のルールをしっかりと読み取らなければならないので、それがテーマのひとつであると考えられます。
移動する面のうちの１つの速度が流動的であることをしっかりと読み取りましょう。

②空間把握能力
２方向からのくり抜きで、重なりが生じるので、それなりの空間把握能力が必要です。
２方向からのくり抜きでそれが重なる場合、「見取り図」を描いて解くやり方もあるのですが、私は「見取り図」はお勧めしません。
むしろいかにして「見取り図」を描かずに解くかが大切でしょう。
結論から言えば空間を平面的に捉えて問題を解決するのです。
本問の場合は特にそれがピッタリだと思います。

③作図→平面的に捉える
②の流れを汲んだ作図となります。
本問は２方向から見た平面図を活用することによってスマートに解くことができます。
やはり「立体図形」の問題は次元を落とし平面的に捉えることが急所になることが多いですね。

④等積変形
円周率が関係する問題は計算が煩雑になることが多いです。
本校は計算が煩雑になることが多く、本問も一瞬嫌な予感が漂うのですが、等積変形を利用することによって計算の煩雑さはほぼ感じることがなくなります。

立体の等積変形は「円すい→円柱」が典型ですが本問の場合は「１部が取り除かれた円柱→円柱」を利用するとうまくいきます。

⑤前の答を利用する
（１）の答を利用することができました。
意図的に数字を作ってあるので、本校は工夫して効率よく解くことができる受験生を求めていると考えられます。
志望校合格の近道は学校側が求めている人物像に近づくことなので、是非本問を参考にしてください。
以上を踏まえて問題を解いてみましょう。

（１）
１辺１０ｃｍの立方体の体積は
１０×１０×１０＝１０００（ｃｍ^３）
そこから７秒動いた円の分（高さ７ｃｍの円柱）の体積を引きます。
１０００－１×１×３．１４×７＝９７８．０２（ｃｍ^３）…（答）

（２）
〈３秒後〉
正面から見た平面図（〈図１〉）を描きます。
〈図１〉

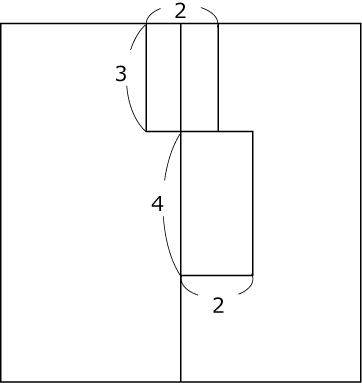
くり抜く円柱と四角柱の重なる部分がないのでそれぞれの体積を引けばよいです。
１０００－（１×１×３．１４×３＋２×４×２×３）＝９４２．５８（ｃｍ^３）…（答）
〈５秒後〉
正面と上面から見た平面図（〈図２〉）を描きます。
〈図２〉正面

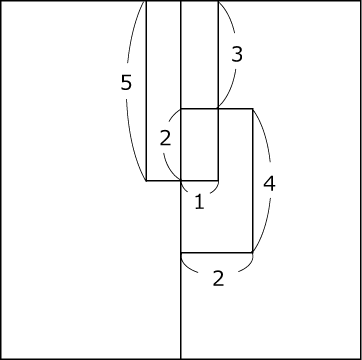
上面

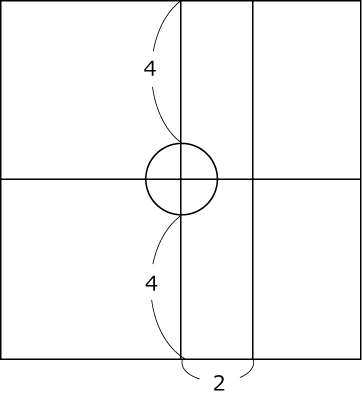
くり抜く円柱と四角柱の重なる部分が底面が半円で高さが２ｃｍの柱体であることがわかります。
これを円柱から引いた形の体積は高さが
５－２÷２＝４（ｃｍ）
の円柱の体積に等しいです（〈図３〉）。
〈図３〉

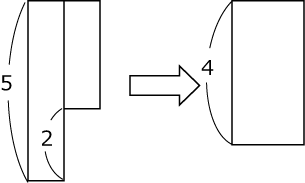
よって
１０００－（１×１×３．１４×４＋８×１０）＝９０７．４４（ｃｍ^３）…（答）

（３）
０．６２５＝  ５  ８  
なので長方形は８秒間で５ｃｍ動きます。
正面と上面から見た平面図（〈図４〉）を描きます。
〈図４〉正面

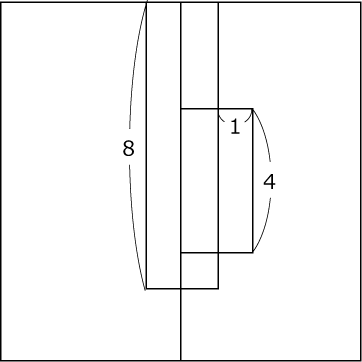
上面

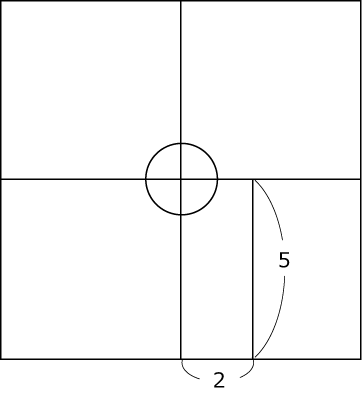
くり抜く円柱と四角柱の重なる部分が底面が四分円で高さが４ｃｍの柱体であることがわかります。
これを円柱から引いた形の体積は高さが
８－４÷４＝７（ｃｍ）
の円柱の体積に等しいです（〈図５〉）。
〈図５〉

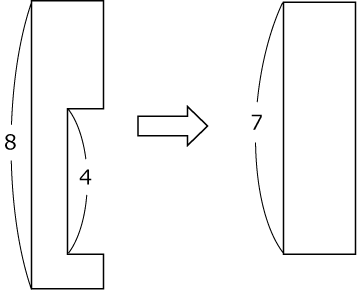
（１）の答が立方体から高さが７ｃｍの円柱を引いたものになっているので、そこから四角柱の体積を引いたものが答です。
よって
９７８．０２－８×５＝９３８．０２（ｃｍ^３）…（答）

（４）
（３）の答よりも２０ｃｍ^３近く小さくなっていますから、四角柱の高さは６ｃｍよりも大きいと考えられます。
円柱から四角柱の重なりの部分を引いた体積は（３）と同じ考え方をすれば
８－４÷４＝７（ｃｍ）
より、高さが７ｃｍの円柱と同じです。
それを立方体から引いた体積は既に（１）で求めています。
それと９２０．４２ｃｍ^３との差が四角柱の体積なので、それを底面積で割れば高さが求まります。
（９７８．０２－９２０．４２）÷８＝７．２（ｃｍ）
それを９秒で動くので速さは
７．２÷９＝０．８（ｃｍ/秒）…（答）
いかがでしたでしょうか。

一見煩雑な計算が待っていそうな問題が、そうでもなかったことに驚いたのではないでしょうか。
立体を平面的に捉え、等積変形を用い、前の計算結果を利用することでかなりの計算量を省くことができました。
こんな風に解ければさらに算数が楽しくなりますね。