VOL.37志望校対策(10) 「駒場東邦」
今回は駒場東邦について書きます。
「新御三家」の筆頭と言われることもある人気校です。
算数の入試問題も難易度が高いことで知られていましたが、近年はやや落ち着いて、取り組みやすくなっている印象を受けます。
さっそく対策にいきましょう。
いわゆる「男子トップ校タイプ」の問題です。
- 制限時間60分で大問4題
- 手を動かして調べ上げるような問題
- 作図や説明の問題
- 途中式・考え方を書く
- 図形の占める割合が高い
以上が特徴として挙げられます。
出題分野は「数論」と「図形」が目立ちます。まずは「図形対策」から考えていきましょう。
どの分野にも言えますが、基本的な問題は完璧に解けるようにしておく必要があります。
知っている範囲のものは瞬時に答まで到達できるようにトレーニングしておくべきです。
さらに、この基本知識をベースに応用問題を解く練習をしておきましょう。
具体例を挙げると、補助線を1本引くことによって基本問題と同じ形になるようなものは、「あたかもその線が引いてあるかのように見える」まで、練習をするということです。
過去問を解くことによって難易度の上限をつかみ、普段の学習ではその少し上までやっておくことも重要です。
学習の深さの調整ですね。
これは「立体図形」で特に重要になります。
「立体図形」は「広さ」はあまりないので、「深さ(難易度)」でそれぞれの学校の特徴を出していると感じられます。
他の男子難関校だと「麻布」や「栄光」には「立体図形」での「深さ」はあまり感じられません。
本校の「深さ」はそれなり(「灘」ほどではないが前記2校よりは深い)なので、「立体図形」で差がつく可能性が高いです。
特に「立体切断」で難易度の高いことが多いので十分に学習しておく必要があります。
以前も書きましたが、「立体切断」はイメージをつかみにくいので、「模型」を作って見せてあげることが効果的です。
本校の平成23年の4番などは模型で見たら感動ものでしょう。
ただし、3×3×3の立方体の積み木は27個必要ですから作るのはけっこう大変です。
私もこれとほぼ同じものを作ったことがありますが、色を塗ったりしたため、完成までに1週間かかりました。
簡単なもので良ければ、慣れてくれば1時間ほどで作れると思います。
また、「立体」は平面で処理することが急所になりますので、そこは徹底してください。
「投影図」や「輪切り方式」等を必要に応じて使えるように十分に練習するようにしてください。
普段の学習では想定される深さをほんの少し超えることを目標とします。
そうすれば、差がつく問題で正解の側にまわることができ、合格の可能性が高まります。
問題のレベルの判断や、到達度の判定は指導者に行ってもらうのが良いでしょう。
特に、到達度の判定は重要で、他分野(他教科)とのバランス調整は時間が限られている今の時期からは特に重要となります。
すでに合格ラインを越えているのにもかかわらず、その分野にさらに多くの時間を割くのは得策ではありません。
理想は全ての分野で合格ラインを越えることですから、あと少しで越えるところを見極め、そこを優先するようにしましょう。
「平面図形」は「広さ」があるので、まずは苦手がないように全体をしっかり固めてください。
その中でも「面積」「相似」といった頻出分野はある程度の難問まで対応できるようにしておきましょう。
また「図形の移動」も頻出なので、しっかりと作図できるようにしておいてください。
コンパスを使った作図が出題されているので、普段からコンパスを使うようにすると良いでしょう。
対策に関してはそんなに神経質にならなくても良く、普段から定規とコンパスを使った作図ができていれば十分です。
次いでもうひとつの主要テーマ「数論」です。
受験算数では「整数問題」等と「規則性」「場合の数」をひっくるめて「数論」と呼んだりします。
中学受験の範囲の中で数学とのつながりが強い分野ですね。
ちなみにもうひとつの大きな分野である「文章題」は数学では「方程式」を使って解くので、関連が断ち切られてしまう分野です。
「図形」はほぼそのままで、発展していくイメージです。
よって、本校は「数学」との関連を重視して出題がなされていると見ることができるでしょう。
※
数学を視野に入れた指導ができる者につくのがベストということになります。
家庭教師は小学生だけでなく、中学生や高校生をみていることが多く、そういう意味では家庭教師に習うのが一番なのかもしれないですね。
「数論」の中では「整数問題」が頻出で「規則性」「場合の数」との融合も見られます。
ポイントになるのは「手を動かす」ことです。
一読しても何を言ってるのかわからない、あるいは解法の糸口がつかめない問題でも、書いているうちにだんだんと見えてくることが多いです。
「躊躇なく書き出す」「粘って解法の糸口をつかむ」というのは経験がものを言いますので、十分な演習量を確保するようにしてください。
このあたりが本校の特徴が最もよく出ているところなので、できれば指導者に練習用の問題の選択や到達度の判定、答案の添削をしてもらってください。
独学の場合は、他の男子トップ校(「灘」「開成」「筑駒」「栄光」「聖光」等)の過去問の中から似たような問題をピックアップして取り組んでください。
ここで大切なのは、正解に至るまでの考え方です。
問題の難易度に対して合格者平均点がやや高いと感じられるので、本校の場合、部分点が多く与えられていると推測されます。
ですから、普段から途中式や図・表・グラフをきちんと書き、自分の考え方を相手に伝えられるような答案をつくる練習をしておかなければなりません。
そして、きちんと伝えられているかどうかは「他者」が客観的に判断するべきでしょう。
その厳しい目をクリアすれば、良い答案が書けるようになっているとみることができます。
最後に「文章題」についてです。
この中で出題可能性が高いのは「速さ」です。
「速さ」に関しては出題されるものと思って準備するようにしましょう。
過去問で難易度をつかみ、普段の学習でその難易度よりもやや上の問題が解けるようなレベルを目標に頑張りましょう。
その他の「特殊算」などは、出題可能性は低いとは思いますが、本校の受験生ならば、「やや難」レベルの問題までしっかりと解けるようにしておいてください。
要するに本校が求める「基本レベル」の問題は全て解けるようにしておくということです。
それではまとめます。
- 「男子トップ校」タイプの出題である。平易な問題に対してスピーディーに解答するということはできて当たり前で、そこからさらに進んで、大がかりな問題を自分の頭を使って解決していくという能力が求められている。
- 出題の2大分野は「数論」と「図形」。いずれも数学に通じるので、そこまでを視野に入れた指導を受けたい。
- 「手を動かす」ことが基本。書いて調べて頭を働かせる。
- 解答に至るまでの考え方が重要。普段から「なぜそうなるのかを意識する」こと。またその考え方を表現できなければならないので、十分に練習する必要がある。
- 難易度が低くなると高得点勝負となるので、ミスが許されない。難易度が高くなると部分点狙いが必要になる。当日の判断で戦略を変える柔軟性が求められる。
今年の問題で「自由記述」のようなものがありました。
学校側がどのような狙いで出題したのかはわかりませんが、少なくとも「算数マシン」ではなく、「算数が好きな人間」が欲しいということは想像できます。
ですから、自分の考え方をアピールできれば点数がもらえる可能性は高いと思います。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の練習問題駒場東邦
難易度★★★★☆
〈図1〉は半径7cmの円の周を6等分し、その弧を1つおきに折り曲げたものです。
それをもとに〈図2〉のような図形をつくりました。
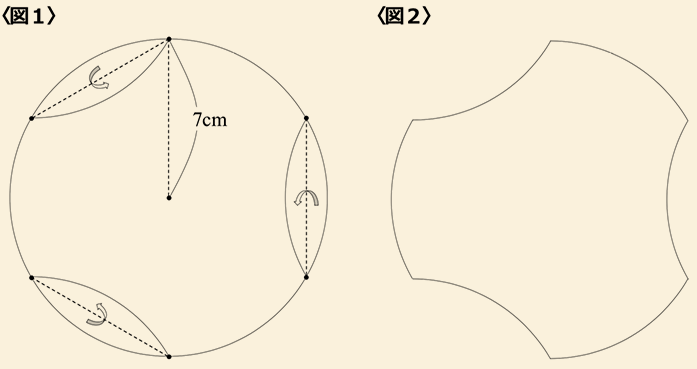
〈図2〉の図形のまわりを円が転がって1周するとき、以下の問いに答えてください。
ただし、円周率は227とします。
(1)
半径1cmの円を転がすとき、円の通った範囲の面積を求めてください。
(注)求める際は、必ず定規とコンパスで作図をするようにしてください。
(2)
半径がacmの円を転がすと、円の通った範囲の面積が147.84cm2になりました。aを求めてください。
解答が表示されます













