VOL.36志望校対策(9) 「栄光学園」
今回は栄光学園を取り上げます。
神奈川が誇る進学校です。
入学後は自然豊かな環境で伸び伸びと学園生活を送ることができます。
算数の入試問題ですが、10年ほど前からコンスタントに良質な問題が提供されており、安心感があります。
学校側の意図がはっきりしており、その意図を反映した問題で差がついていると考えられます。
対策は「学校側に欲しいと思わせる人材になる」ということに尽きるでしょう。
具体的にどうすれば良いかを考えていきます。
本校の試験は、パターン問題しか解けないのでは全く歯が立たず、その場でどれだけ頭を使えるかを見るものが多いです。
名物とも言える「論理」の問題にそれが良くあらわれています。
平成20年に出題者の覚悟を感じさせるような超難問が登場したのですが、さすがに難しすぎました。
翌年から難易度の調整の苦労が始まり、その甲斐あって近年は質量ともにちょうど良く、実力差がきちんと反映される試験が続きました。
今年は合格者平均点が8割近かったのですがこれは異例なことです。
前年が6割を切っていたので、難易度の調整をしたところ、受験生が思いのほか優秀でこのような結果になったのだと思います。
この傾向はどの学校にも当てはまり、少し問題が簡単になると途端に高得点勝負になります。
どの受験生もきっちり仕上がっているという印象です。
ここで重要なのは、難易度はふたを開けてみなければわからないということです。
ですから準備の段階では「基本的な問題は満点を取る」という意気込みが必要です。
その上でその場で考える問題、未知なる問題にどう対応するか準備しておくのです。
学校側がどのような人材が欲しいかを考えてみます。
出題されている内容から以下のような人物像が浮かび上がってきます。
①
自分の頭で考えることができる
②
未知のものにチャレンジすることができる
③
困難なものに対し粘り強く取り組むことができる
④
自分の考えを相手に正しく伝えることができる
⑤
基本的なことを当たり前のようにこなすことができる
こうやって並べるとかなり優秀な人物に思えてきますが、本校を目指すのならば、ここに近づかなければなりません。
今までも書いてきましたが①~④に必要な「力」を養成するには、初見の問題に対し精一杯取り組む必要があります。
本校の場合それが特に重要で、「問題文の内容を読み取る力」「図・表やグラフを書く力」「諦めずに粘る姿勢」や、「自分の考えを表現できる記述力」をしっかり養っておくべきです。
そして、これらの練習をするのに側に指導者がいるといないとでは大違いということも書いてきました。
特にこれからの時期は時間とのたたかいなので、できれば指導者のもとで効率よく学習してもらいたいと思います。
練習のためには初見の問題が必要ですが、過去問の1回目は非常に良い練習になります。
それが終わった後は他校の問題ということになりますが、テイストが違うことが多く、効果的な練習にならないかもしれません。
そこでおすすめしたいのが本ブログの「今週の1題」です。
本校が要求している能力を鍛えることができる問題が載っている回を記しておきます。
どれも実際の試験で出題されればいきなり解かずに後回しにすべきレベルですが、そういった問題に対して粘り強く取り組み、解法の糸口を見出すような練習をすることで「力」がついていきます。
ただし、今は時期的に「制限時間なし」というわけにはいかないので、程よいタイミングでヒントを出す等の軌道修正が必要なことが多いでしょう。
やはり、指導者のもとで行ったほうが、リスクが低いと思います。
独学の場合は時間を決めて、時間内に解けなかった場合は解説を読んで理解するようにしてください。
※
5年生以下の生徒さんが「今週の1題」に取り組む場合は「制限時間なし」がむしろおすすめになります。
何日も考えた末に解けたといった経験は、算数に対する自信を生み出します。
最後にまとめます。
- 基本が大切なのはどの学校でも同じ。「基本的な問題は全て解ける」という自信をもって試験会場入りできるように準備しておくこと。
- 初めてみるような問題に対し、落ち着いて対応すること。問題をよく読み、手を動かすことによって糸口がつかめる。
- 難しいと感じたら、一旦後回しにすること。戻った後は粘って少しでも多く点数を稼ぐこと。
- 視野を広く持つこと。例えば、極端な例で実験し、そこから全体像をイメージできるように。
- 頭を柔らかくする。そしてなによりも算数を楽しみ、好きになること。
そうです。本校は「算数大好き少年」を求めているのです。
算数が好きなら可能性はあります。最後まで諦めずに頑張りましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の練習問題栄光学園
難易度★★★☆☆
名門くんと栄くんの二人は鬼ごっこをすることにしました。舞台は〈図1〉のような道です。四角形ABCDとEFGHはともに正方形で、1辺の長さはそれぞれ7mと5mです。またAFは3mです。また1~10の点は各辺を7等分した点上にあり、1m間隔で並んでいます。
栄くんは点Eから、名門くんはB、G、C、Hあるいは1~10までの中からひとつを選び、二人は同時にスタートします。二人の速さは同じで秒速1mです。
最初、栄くんは正方形EFGH上を反時計まわりに進み、名門くんは正方形ABCD上を反時計まわりに進みます。
二人がどちらかの正方形の同一辺上に来た瞬間から、栄くんは道を自由に選べるようになります。進行方向を変えてもかまいません。それに対し、名門くんは今までと同じ動きを続けます。
二人が出会えばそこで鬼ごっこは終了となります。ただし栄くんは二人が最も早く出会うルートを選ぶものとします。
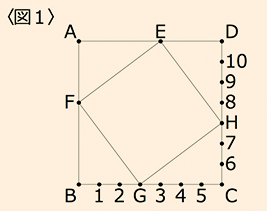
(1)
名門くんがGからスタートした場合、二人は何秒後に出会いますか。
(2)
二人が出会うのが最も遅くなるのは名門くんがどの点を選んだときですか。また、そのとき二人はスタートしてから何秒後に出会いますか。
解答が表示されます













