VOL.38志望校対策(11)「筑波大学附属駒場」
今回は「筑駒」をとりあげます。
中学受験において、都内男子校の最高峰でしょう。
「開成」合格レベルの受験生だけで、わずかな椅子を奪い合うようなイメージです。
厳しいたたかいですが、対策を考えていきたいと思います。
まず、本校の算数は普通にやっていたらほとんど歯が立たない、無理気味な試験であるということを知っておきましょう。
「慣れ」がないとまず時間が足りなくなります。
受験生の層がトップレベルなので、その中で差をつける問題となると、どうしてもそのようになってしまうのですね。
ですから、受験生側の心得としては、他校(例えば「開成」)の対策を十分に行ったうえで、本校の出題傾向に慣れるという姿勢が望ましいと思います。
ここからは2月1日の受験校が「開成」であることを前提に話を進めていきます。
「開成」対策で「思考力」や「正解力」は十分に獲得できているはずです。
そうでなければ、本校を受けること自体がやや危険(2月3日に押さえの学校を受けられなくなるので)だと思います。
一般的な試験では十分な実力を持つ受験生が本校の対策を行う場合何が一番大切かというと、それはずばり「思い切りの良さを身に付ける」ことだと思います。
本校の試験は「筑駒ワールド」と呼ばれることもある、独特の世界がひろがります。
それは「規則性」の問題に良くあらわれていて、躊躇なく書き出し、丁寧に調べないと全く歯が立ちません。
「躊躇なく書き出す」というところが意外と難しく、特に、高いレベルの思考力を獲得している受験生には、普段と逆の姿勢を強いられていると感じることもあるようです。
どうしても先のことを考えたくなってしまう気持ちを抑え、まずは「書く」、これが本校の試験で求められている姿勢です。
「書く」となるとその書き方も重要です。
本校の場合、解答用紙に計算のスペースがあり、その横に答を書き込むようになっていますが、まずは問題用紙の空きスペースを使うことになります。
解答用紙の「計算」は解いた後に必要最低限のものを転記するのが良いでしょう。
この「空きスペースの利用」がキーになります。
ここをうまく使えるかどうかで合否が決まるといっても過言ではありません。
「適正なサイズで見やすく書く」と言葉にすると簡単ですが、やってみると難しいです。
そもそも「適正なサイズ」とはどのくらいなのか、どこから書けばよいのか等悩みは尽きません。
これらを思い切りよく処理できるようになるためには「回数をこなす」しかありません。
しかもただやれば良いのではなく、自分のやったものを手本となるようなものと照らしあわせ、もっと良くするにはどこをどうすれば良いかを検討し、その反省を次に生かす、といったことを反復する必要があります。
ここでネックとなるのが「手本となるようなもの」です。
通常の教材には載っていないでしょうし、赤本の解答を見てもあまり参考にならないでしょう。
やはり、指導者に頼るのが最善ということになります。
実物大ということになると「集団指導」では無理なので、「個別指導」しかないかもしれません。
ただし、指導者が手本となるようなものを作るだけの「実力」がなければ意味がないので、それだけは気をつけてください。
厳しい言い方かもしれませんが、中学受験の専門家以外が指導しても効果がない(むしろマイナス?)と思われます。
指導者に手本となるようなものを用意してもらえたら、後はひたすら練習です。
書いて書いて書きまくり、体に染み込ませるイメージです。
書いたものを「手本」を見て修正し、それを次に生かすということをやっていると、自分なりのスタイルというものが身についてきます。
そのスタイルが固まってきたら準備が整ったといえるでしょう。
それではまとめます。
- トップ中のトップが集まるので他の受験校の対策は万全で当たり前である。
- 「思考力」「正解力」ともに最高レベルのものが要求される。
- 「思い切りの良さ」を身に付けなければならない。
- 「躊躇なく書き出す」→「丁寧に調べる」といった流れを繰り返し練習する。その際指導者が上質な「手本」を示さなければならない。
- 自分なりのスタイルが固まってくれば準備が整ったといえる。
本校は本当に厳しい受験で、受かった当人の感想が「運が良かった」ということも多いです。
ただ、私はそういう人こそ「実力」で受かったと思うのです。
受かってもなおその謙虚な姿勢、すばらしいの一語です。
本校の試験は「人間」そのものを試されているのかもしれません。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の練習問題筑波大学附属駒場
難易度★★★★☆
a×aの正方形のマス目に以下に示した操作にしたがって数字を入れていくということを何回か行います。ただしaは奇数とします。
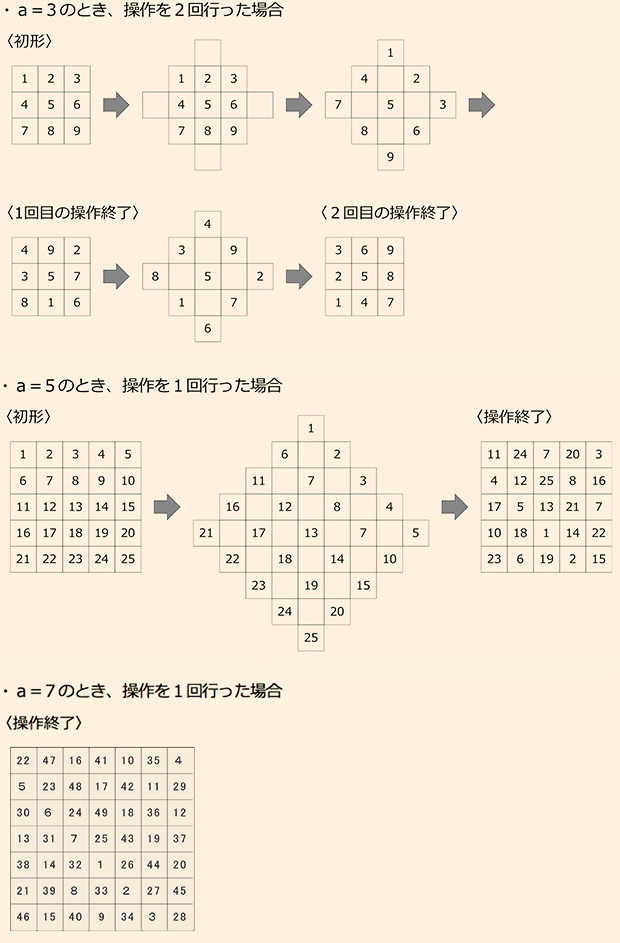
(1)
操作を1回行ったところ、いちばん上の段の左から2番目のマスに219が入りました。いちばん下の段の右から2番目に入っている数字を答えてください。また、いちばん右の縦1列に入っている数字の合計はいくつになりますか。
(2)
操作を2回行ったところ、対角線の交点に当たるマスのひとつ上のマスに231が入りました。このときのaはいくつですか。
(3)
a=11のとき、この操作を2018回行うと、「1」は上から何段目の左から何番目に入りますか。
解答が表示されます
(1)7、1695(2)21(3)上から9段目の左から3番目













