VOL.238数学から考える受験算数(4)ピタゴラスの定理
数学には「定理」というものがあります。
「定理」とは証明されている命題のことです。
ここでは命題とは何かといったことは省きますが、数学を学ぶ上では言葉の意味の理解は重要です。
図形においてとても役立つ「定理」の1つに「ピタゴラスの定理」があります。
多分最も有名な「定理」で小学生も多数が知っていると思います。
今回はこの「ピタゴラスの定理」がテーマです。
「ピタゴラスの定理」は「三平方の定理」とも呼ばれます。
「直角三角形において、斜辺の2乗は他の2辺をそれぞれ2乗したものの和に等しい」という比較的シンプルな内容ですね。
この定理は多数の証明が知られており、数百通りもあると言われています。
頑張れば何とかなりそうではあるのでチャレンジしてみるのもよいでしょう。
さて、直角三角形は3辺のうち2辺の長さがわかれば残りの1辺の長さをこの定理を使って求めることができるわけです。
では中学受験で3つめの辺の長さを求められることが有利に働くかというと、かなり限定的な気がします。小学生は扱える数字が正の有理数なので、以下で述べる整数の比になるようなケースしか長さを求めることができません。
ルートを学べば対応可能ですが、そこまではやらないことを前提に話を進めます。
「ピタゴラスの定理」を満たすような自然数の組を「ピタゴラス数」と呼びます。
中学受験でよくでてくるのが(3,4,5)で、次いで(5,12,13)、(8,15,17)、(7,24,25)まで位なら見かけることがあります。
個人的にはここまでは頭に入れておくと良いとは思います。
他で見たことがあるのは(20,21,29)ですが、覚える必要はないと思います。
ピタゴラスの定理を知っていれば有利になる問題をひとつやってみましょう。
【例題1】
縦4cm横10cmの長方形が内接している円の面積を求めてください。
※以後円周率は3.14とします。
【解説】
底辺が10cm、高さが4cmの直角三角形の斜辺がこの円の直径にあたります。
ということは5cm、2cmの直角三角形の斜辺がこの円の半径となります。
半径×半径=5×5+2×2=29
29×3.14=91.06(cm2)…(答)
このように「ピタゴラスの定理」が使えれば明らかに得になります。
ただ、正方形の内部に斜めに内接する正方形を描けば解けるので、「絶対に覚えるべし」とまではいかないでしょう。
【例題2】
〈図1〉の四角形ABCDはAD平行//BCの台形です。台形ABCDをDCを軸として1回転してできた立体の体積が19154cm3でした。
AD=20cm
BC=25cm
のとき、この立体の表面積を求めてください。
【解説】
ⅰ)一般的な解き方
〈図1〉
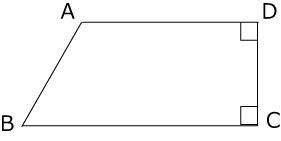
〈図1〉のABとDCを延長し、その交差点をEとします。
〈図2〉
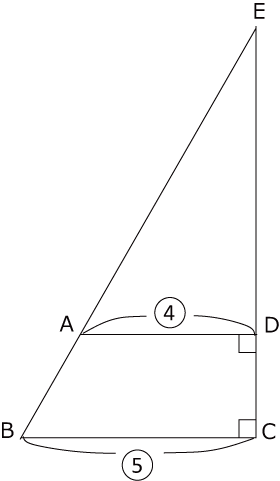
〈図2〉の直角三角形EBCをECを軸として回転させたときの上部と下部(ADを含む底面と平行な面で分ける)の体積比は
4×4×4:5×5×5-4×4×4
=64:61
よって三角形EADをEDを軸として回転してできる円すいの体積は
19154× 64 61 =3.14×6400(cm3)
よってEDの長さは
3.14×6400×3÷(20×20×3.14)=48(cm)
〈図3〉
正方形
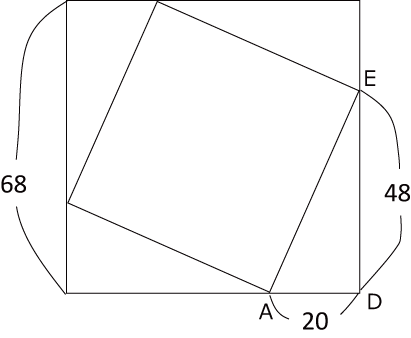
〈図3〉より
EA×EA=68×68-48×20×2
=2704
=52×52
なので
EA=52(cm)
EC=48× 5 4 =60(cm)
EB=52× 5 4 =65(cm)
以上より表面積は
65×25×3.14-52×20×3.14+20×20×3.14+25×25×3.14
=1610×3.14
=5055.4(cm2)・・・(答)
ii)ピタゴラスの定理を利用
上でED=48(cm)が求まったところでDCを求めます。
DC=48× 1 4 =12(cm)
ここでAからBCに垂線を下ろし、その交点をFとします。
〈図4〉
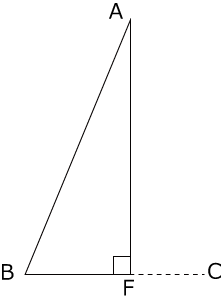
△ABFは直角三角形で
AF=12(cm)
BF=25-20
=5(cm)
なので、5:12:13より
AB=13(cm)
側面積をセンターラインを使って求めると
(20+25)×3.14×13=585×3.14(cm2)
ふたと底を足して
(20×20+25×25+585)×3.14
=1610×3.14
=5055.4(cm2)・・・(答)
かなり労力が省けたと思います。
下手をすると.「BFが5cmなんだからABは13cmの可能性が高い」というカンが働けばいきなり最後の式を立てることも可能です。
最後に小学生特有の問題についてお話しします。
「ピタゴラスの定理」からも明らかなように三角形の3辺のうちの2辺が自然数でも残りの1辺は自然数とはかぎりません。ほとんどが根号がついた数字になります。
であるならば、小学生時代は長さが「不明」ということが多いのですね。
当然、近似値で与えられることはありますが、正確な数字は習うことがありません。
しかしながら、その「不明」な数字を求めようとして迷路に迷い込む受験生が多々います。
具体的には
・正三角形の1辺がわかっているときの高さは「不明」
・正方形の1辺がわかっているときの対角線は「不明」
の2つが代表例です。逆もいえることは直感的にわかると思います。
ですから、これらを何とかして求めるようなことはしないようにしましょう。
他の方法で解けるようになっていますよ。
最後にまとめます。
・「ピタゴラスの定理」は、そんなに難しくないので理解はしておいた方が良い。
・そこから必然的に導かれることも重要である。
①直角三角形は2辺が決まれば残りの1辺も決まる
②基本的に2辺が自然数の場合、残り1辺は不明であることがほとんど。ただし、その長さを1辺とする正方形の面積は「ピタゴラスの定理」そのものと言える。
・「ピタゴラス数」は小さい方から4組ぐらいは頭に入れておいたほうが得になることが多い。
無数にあるのであまり深追いはしないこと。
今回は結論が割とはっきりしていたと思います。
有利になりそうなところまでやっておけば良いのです。
※根号をどうするかについては改めて検討してみたいと思います。
また、中学入試で直角三角形がテーマの問題は頻出です。
今回の「ピタゴラスの定理」はその証明が問題として取り上げられることもあるので、今週の1題で練習してみてください。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題ピタゴラスの定理
★★☆☆☆
次の文章はピタゴラスの定理を証明するものです。
下記の□に当てはまる文字または数字を求めて下さい。〈図1〉で三角形ABCの面積をS、内接円の半径をrとおきます。
〈図1〉
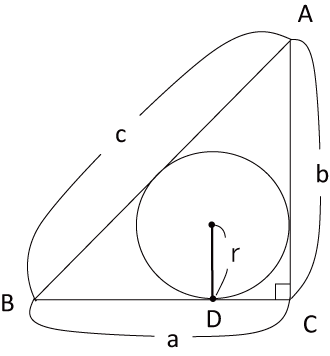
S= 1 2 ×a×b
= 1 2 ×ア×(a+b+イ)
また、内接円とBCとの接点をDとすると
r=CD= 1 2 ×(a+ウーエ)
です。
よって
a×b= 1 2 ×(a+ウ-エ)×(a+b+イ)
整理すると
オ×a×b=(a+b)×(a+b)-c×c
c×c=(a+b)×(a+b)-オ×a×b
〈図2〉
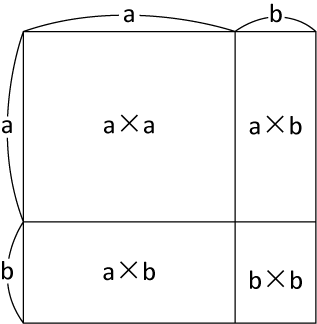
〈図2〉より
c×c=カ×カ+キ×キ
となり、ピタゴラスの定理を得ることができました。
解答が表示されます













