VOL.239数学から考える受験算数（５）関数

私が「関数」を初めて習ったとき、全く訳がわかりませんでした。
何を何のためにやっているのかピンとこなかったのです。
さすがに「２次関数」あたりまで進んで（特にグラフとｘ軸の交点の座標が方程式の解ということを学んだ頃）、「関数」の重要性がなんとなく見えてきました。

高校数学で「関数」が占める割合は、大人の皆さんにおいては承知されていることと思います。
大学受験では「関数」が苦手は即アウト級ですね。

さて、受験算数で「関数」に似た分野として「２量の関係」があります。
また、「比例・反比例」は「関数」に含まれる分野です。

ですから、今回のテーマは上記の分野において「数学」をどれ位取り入れたらよいか、ということにしたいと思います。

まず、関数の定義を確認していただきます。

◎ｘの値が決まるとｙの値が１つに決まるとき、ｙはｘの関数である。

基本的に、ｘとｙの間に法則のようなものがあればｘが決まればｙを求めることができるということです。

それでは例題をみていただきましょう。

〈例題１〉
ＡはＢに比例し、ＢはＣに反比例します。Ａが２５のときＢは５、Ｂが１のときＣは２です。
それではＣが５のときＡはいくつですか。

〈解説〉
小学生が習うのは以下になります。

・比例…片方が２倍、３倍、４倍となるにつれ、もう片方も２倍、３倍、４倍となるような関係

・反比例…片方が２倍、３倍、４倍となるにつれ、もう片方は  １  ２  倍、  １  ３  倍、  １  ４  倍となるような関係

これを使うと
Ｃは２を基準にすると
５÷２＝  ５  ２  
より、  ５  ２  倍になっているのでＢは  ５  ２  の逆数である  ２  ５  倍。
１×  ２  ５  ＝  ２  ５  
よりＢは  ２  ５  。

Ｂが５を基準にすると
  ２  ５  ÷５＝  ２  ２５  （倍）
になっているのでＡも  ２  ２５  倍。
よって
２５×  ２  ２５  ＝２　…（答）

という具合で、何となく煩わしいような気がします。

これに対し数学では比例と反比例の関係式が決まっていますからそれに代入すれば本問は自動的に解けます。

・比例…ｙ＝ａｘ（ａ≠０，ａは比例定数）

・反比例…ｙ＝  ａ  ｘ  （ａ≠０，ａは比例定数）

比例の式を変形すると

  ｙ  ｘ  ＝ａ

となり、比の値が一定ということになりますし、反比例の式を変形すると

ｘｙ＝ａ

という小学生にとってわかりやすい、積が一定ということになります。
これらの式を利用すれば

Ａ＝５×Ｂ　　…①
Ｂ＝  ２  Ｃ  　　…②

となり、②にＣ＝５を代入して

Ｂ＝  ２  ５  　　…③

③を①に代入して

Ａ＝５×  ２  ５  　
　＝２　…（答）

となり、むしろ解りやすかったかもしれません。
「比例・反比例」の式を学ぶのは悪くないと思います。

〈例題２〉
５０ｇのおもりをつるすと全長が２５ｃｍになり、８０ｇのおもりをつるすと全長が２８ｃｍになるばねがあります。このばねの自然長を求めてください。

〈解説〉
ばねはおもりの重さと伸びが比例の関係になります。５０ｇ⇒８０ｇは３０ｇ重くなっており、そのとき２５ｃｍ⇒２８ｃｍと３ｃｍ伸びています。

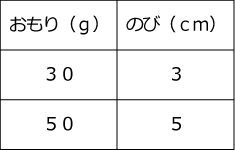
２５－５＝２０（ｃｍ）…（答）　
これを数学的に考えてみましょう。

・解法１
ばねはおもりの重さ（ｘ）と全長（ｙ）の関係は１次関数になるので
ｙ＝ａｘ＋ｂ　…①
とおける。
これに（ｘ，ｙ）＝（５０，２５），（８０，２８）を代入して連立方程式をつくる。

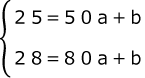
これを解いて
ａ＝  １  １０  ，ｂ＝２０
よって
（答）２０ｃｍ

・解法２
座標上の２点（５０，２５），（８０，２８）を通る直線の式のｙ切片の値が答なので
変化の割合から傾きを求める公式を利用して
ｙ－２５＝  （２８－２５）  （８０－５０）  ×（ｘ－５０）
ｙ＝  １  １０  ×ｘ＋２０
より
（答）２０ｃｍ

実は、小学生的な解き方は数学の解法２とほぼ同じなのでした。
「１次関数」で素早くできなければならないことの１つに、２点を通る直線の式を求めることが挙げられますが、小学生的な感覚がスピードを高めてくれるのですね（連立方程式は遅い）。

ということで、「１次関数」に関しては「数学」に頼る必要はないという結論とさせていただきます。
その他、２量の関係では複雑な問題もありますが、数学で学ぶ「関数」の知識が必要かというとそうでもないように思います。

グラフはほとんど同じと考えることもできますが、小学生は第１象限しか扱わないという大きな違いがあります。
「関数」に関しては「比例・反比例」は別として指導者が意識しておけば良く、本人は「算数」的に考えれば良いと思います。