VOL.35志望校対策(8) 「灘」
関西の雄「灘」です。日本を代表する進学校と言っても良いでしょう。
算数の入試問題ですが、その圧倒的なクオリティーで、受験界をリードしています。
他校にない特徴としては、算数の試験は2日かけて行われ、「1日目」と「2日目」では要求される能力が明らかに異なることが挙げられます。
実に厄介です。
特に「1日目」の対策が難しいです。
「2日目」の対策だけなら今までも出てきた「男子トップ校」向けのもので良いのですが・・・。
※ 逆に言えば、ある程度のレベルに到達した受験生が「1日目」対策をきちんと行えば、合格の可能性はかなり高まると考えています。
なぜ「1日目」かと言うと、「1日目」に失敗すると「2日目」に力を発揮することが難しくなってくるからです。
また、「1日目」の問題はシンプルであり、かなりの処理能力が要求されます。
それだけに慣れておかないと全く歯が立ちません。
時間が足りなくなってしまうのです。
「1日目」を中心に対策を考えていきましょう。
昭和の時代と現在では難易度が明らかに違います。
これは、出題する学校とそれに対応する受験生のせめぎ合いの中で少しずつレベルが上がり、今日に至ったと捉えることができます。
合格者平均点を見ていると過去に何度か明らかな高得点勝負の年がありました。
受験生側の対策が功を奏したわけです。
「さすがの灘もネタが尽きたか」と思われましたが、翌年から新たな段階にステップアップし、クオリティーが上がるということの連続でした。
これは今後も変わらないでしょう。
問題を3つに分類してみます。
① 頻出の問題
② 既視感はあるが切り口が通常と異なる問題
③ 見たことのない問題
どんなに難易度が上がろうと①が多くなれば、高得点勝負になるのが「灘」の入試です。
②が多いと合格者と不合格者の差が開くことになります。
平成17年はこれに当たります。
③が多いと合格者平均点が下がります。算数で差をつけたい受験生には有利になります。
対策としては①~③がどのような割合であっても対応できるように準備しておくということになるでしょう。
そこでまず大切なのは「過去問演習」です。
見たことがあるような問題はほぼ全員が正解ですから、過去に出題された問題は「常識」としておく必要があるでしょう。
これで①の対策とすることができます。
例としては、少し古めの過去問を分野別に並び替えて、単元ごとに繰り返し学習するというやり方があります。
次に②の対策ですが、これは学習の「質」を上げて対応します。
いつもの学習に「幅」と「深さ」を持たせるのです。
「幅」とは同じ考え方で対応できる範囲のことであり、それを拡げることを普段から意識します。
「深さ」とは難易度のことであり、問題文の複雑さや、未知数の位置の変化にも対応できるように準備しておきます。
さらに、別解を模索し、比較検討する姿勢も大切です。
「図形」や「場合の数」では別解が重要な役割を果たすのは言うまでもありませんが、本校の場合は「文章題」で特に重要になっています。
最初の切り口がうまくいかない場合の「プランB」を繰り出せるかどうかで結果が変わる可能性があります。
また、普段から別解を比較検討していれば最初の方針を誤る危険性が下がります。
なんとなく「センス」に頼るのではなく、「理論的思考」を研ぎ澄まし、最初の一歩を誤らないようにするのです。
この学習の「質」を高めることは自分一人では難しい面があります。
やはり指導者のもとで行うのが効率的でしょう。
最後に初見の問題に対応するにはどうしたら良いかです。
これは、どれだけ自分の頭を使って考えたかということになるでしょう。
色々な問題に挑戦し、書いて、粘って、といったことの蓄積が「力」になります。
手前味噌ではありますが 、「今週の1題」は本校の受験生のレベルにも対応できますので、ぜひ解いてみてください。
続いて分野について考察します。
年度によっては分野が偏ることがあります。
しかし、対策としては各分野まんべんなく準備しておく必要があるでしょう。
「2日目」に目を向けると「立体図形」が最重要分野であり、次いで「場合の数」、「平面図形」、「数の性質」と続きます。
「立体図形」は得意分野にしておきましょう。
以前から書いていますが、「立体図形」はやればできる分野です。
本校志望者ならできるはずです。
「場合の数」は対策が遅れている分野として一番最後まで残ってしまうかもしれませんが、それはそれで仕方ないと思います。
無理に「場合の数」に取り組むよりも、他の分野の対策に徹したほうが良いことも多いでしょう。
このあたりは個々の事情によるので、ケースバイケースです。
「1日目」の実践的な練習の仕方について少々書きます。
ある大手塾では制限時間を20分短縮して過去問を解くという練習をしているそうです(私も生徒に時間を10分短縮して「1日目」の過去問を解いてもらう練習をしました)が、これは「1日目」では特に効果的だと思います。
時間を短縮すると、全部を解く時間がなくなりますから、取捨選択をすることになります。
また解答順も解けそうなものからということになり、効率が良くなります。
スピードの絶対値が上がる効果も期待できるでしょう。
私がお勧めしたいのは、解答順をある程度決めておくというものです。
問題を見てみないとなんとも言えないところではありますが、少なくとも「計算はいちばん最初に解く」といったようなことは決めておくべきです。
仮に、私自身が受けるならば、「立体図形」から解きます。
序盤が特に重要なので、得意な分野から入るのが良いのです。
ちなみに「場合の数」は最後にとっておきます。これはお楽しみですね。
過去問演習で色々な解答順を試し、自分に合ったものを見つけておいてください。
まとめです。
1.最上級の試験である。心して臨むこと。
2.苦手分野はあってはならない。少なくとも「立体図形」は得意分野にしておく。
3.「2日目」は男子トップ校対策で可。ただし、難易度は最高レベルなので、準備も最高レベルが要求される。
4.「1日目」対策がカギ。独特の問題に慣れることと、普段の学習の「質」を高めること。時間不足の心配がないレベルまで実力をつける必要がある。
5.過去問演習では「時間の管理」、「解答順」、「取捨選択」等を適切に行えるように意識する。
本校は個人的に思い入れのある学校です。
目指す価値は大いにありますが、狭き門でもあります。
合否は本当にわずかの差で決まります。
その数点の上積みのお役に立てればこれ以上の幸せはありません。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の練習問題灘
難易度★★★★☆
正多面体とは、すべての面が同一の正多角形で構成されており、かつすべての頂点において接する面の数が等しい凸多面体のことをいいます。 正四面体、立方体、正八面体はどれも正多面体です。
図形の重心とはその点で図形をピン止めすれば完全に釣り合うような点です。正三角形の重心は(図1)のGの位置にあり、正方形の重心は対角線の交点にあります。
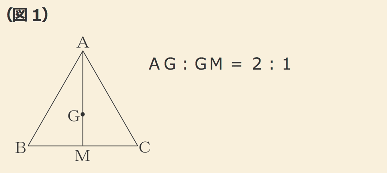
今、体積の等しい3つの立体P、Q、Rがあります。Pは正四面体、Qは立方体、Rは正八面体です。
この3つの立体の中から一つを選び、以下の二つの操作のうちどちらかを選び別の立体を作ります。その後も出来上がった立体に対しても操作を行い、別の立体を作っていきます。
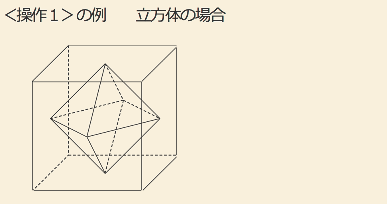
<操作1>
正多面体の各面の重心に頂点を取り、それらを結んで正多面体をつくる。
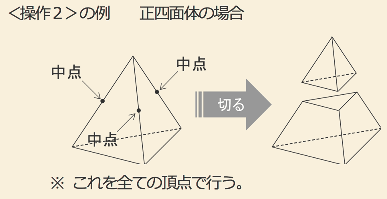
<操作2>
各頂点を辺の中心まで切り落とし立体をつくる。
(1)
<操作1>、<操作2>、<操作1>、<操作2>と合計4回操作を行ったところ、出来上がった立体が初めて正多面体ではなくなりました。 その後さらに3回<操作2>を行いました。 最初の立体はP、Q、Rのどれでしたか。 また、最後に出来上がった立体の辺の数は何本ですか。
(2)
4回操作を行ったところ、出来上がった立体が初めて正多面体ではなくなりました。 その後1回<操作2>を行った後の立体の体積はPの体積の何倍ですか。 考えられるものの中で最小と最大を答えてください。
解答が表示されます













