VOL.229１問全力投球（１２）　桜蔭中　特徴とは？　　

中学受験も試験が終わり、一段落となりました。
受験生の皆さんもリフレッシュされたことでしょう。
今度は中学生活が始まりますから、そちらに「全力投球」をしていきましょう。

ということで、当ブログではしばらくの間【１問全力投球】をやっていきたいと思います。
今回は女子の最難関校の一つである「桜蔭」を取り上げたいと思います。
何を取り上げるか迷ったのですがⅠの（３）に決めました。
まずは問題をみてください。

今年度の問題も本校の特徴がよく表れていました。

結果として、意外と点数が取りにくく、試験に強いタイプが選抜されることになっていると思います。
少し解説を加えます。

①難しい問題が少ないというのは、例えば解説を聞けばわからないということがほとんどないということです。（男子のトップ校では本質的に難しい問題を出すところが結構多いと感じます。）
本年ではⅡが基本問題でした。

②これは対策の上で非常に重要です。
ここ何年か、純粋な「平面図形」の問題はほとんど出題されておらず、「立体図形」がメインであることからも上級分野からの出題が多いことがわかると思います。
また、複数の分野にまたがる問題も多く、本年ではⅣが「推理・論理」「立体図形」「不定方程式」等の要素が入った問題でした。

③本年はそれほどでもありませんでしたが、整数だけですんなり計算できるようなことはあまりなく（本年ではⅠ（２）②がすんなりいく問題でした）、ⅢやⅣのように分数や小数の計算を強いられることが多いです。

④軽い気持ちで解くとすぐに間違えてしまうのが本校の特徴です。
本年ではⅢ、Ⅳがそのタイプの問題で、かなりトレーニングを積んでいないと間違える可能性が高いですね。

⑤試験においては、絶対に合っているという確信があると次の問題に移るときに勢いがつくのですが、それがないとモヤモヤを抱えたままになるので、精神的にキツイです。
それを乗り越えられる強さを身に着けておく必要がありますね。

ということで、今回取り上げるⅠの（３）ですが、この問題は合格レベルの見極めに最適と判断しました。

合格レベルの基準ですが、
「エ」はほとんど時間をかけずに解け、
「オ・カ」は知っていた（女子中で類題の出題例があります）か、あまり時間をかけずに解けた、
というのが合格ラインだと思います。

ですから、本問が
「わからない」
「間違えた」
「時間がかかってしまった」
という場合は、それなりの対処をするべきだということになります。

〈解説〉
フィボナッチ数列の応用問題です。
以後すべて表に整理することにします。

①１つ目が２、２つ目を□として表をつくります。

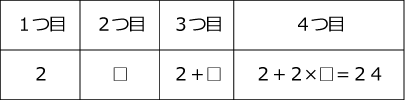
よって「エ」は
（２４－２）÷２＝１１　　　　エ　１１　…（答）

②１つ目をＡ、２つ目をＢなどと置いてとくことも可能ですが、何か方程式を解いているようで気が引けるので、別のやり方でやってみます。

「１つ目を１と２、２つ目を０」と「１つ目を０、２つ目を１と２」の表を書いて調べてみます。

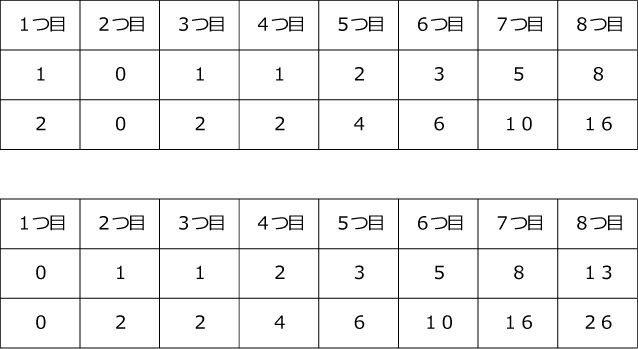
以上の検証から８つ目の数は１つ目の数の８倍と２つ目の数の１３倍の和であることがわかります。
１６０は８の倍数ですから、２つ目の数は８の倍数となり、１６０（８×２０）以下であることから必然的に８と決まります。
１つ目の数は
（１６０－８×１３）÷８＝２０－１３＝７
オ　７　　カ　８　…（答）

解説を読めば誰もができると思ったでしょう。
これも本校の特徴で、実際に正解できるかどうかが問われる試験なのです。

本校を目指す受験生はこの「合格レベル」を意識して勉強に励んでください。