VOL.2301問全力投球(13) 女子学院中 攻略のコツは?
今回の「1問全力投球」は「女子学院」をとりあげます。
本校の算数の問題はそんなに難しくはないという評価が定着しているように思います。
私の見方は時間との兼ね合いで厳しい試験という認識であることは、以前にも書きました。
本校はやや極端な傾向がみられるので、入試問題の難易度が合否にどれ程影響しているかということを考える必要があるでしょう。
以前、灘中を調べ、難易度が変化しても受験者平均点と合格者平均点との差がほとんど変わっていないことから、全体としてはあまり影響がないという結論を出しました。
では本校はどうかというと、
易しい問題の対策しかしていないところに、2019年のような難易度の出題があった場合、一定数の受験生が大崩れしてしまいダメにしてしまう可能性があると思います。
実際、その後3回試験が行われましたが、結局従来の難易度に落ち着いています。
そもそも「時間」が厳しいのですから選抜の目的は十分に達成できるはずです。
単純に問題を難しくすると逆効果になると考えられるので、今後も40分という時間であるならば難易度は現状維持ではないかと考えています。
ただし、対策を立てる上では、少し難しいところまでやることによって、安定度を増すようなやり方が良いように思います(VOL.90を参照してください)。
仮に難化したとしても対応しやすいというメリットもあります。
前置きが長くなってしまいましたが、2022年3.を見てください。
本校では「推理・論理」の問題は頻出ですが、対策をどうしたらよいか、今一つはっきりしない分野と言えるかもしれません。
今回は私がどのように考えたのかを通して、理論的な考え方というものを学んでいただきたいと思います。
〈解説〉
どこからほぐしたら良いか悩ましいですが、
「的を外した人はいない」
「2回以上同じ点数を取った人はいない」
「3人それぞれの最も低い点数は全て異なっていた」
ことから、最も点数低い点数は
「1点・2点・3点」
であり、最も低い点が3点の人の他の2回の点数は
「4点・5点」
と確定します。
なぜ確定するかというと、的には1・2・3・4・5(点)の5種類しかありませんから、上記のように決まるのですね。
「K子の1回目は1点」からJ子が3点を取り、最終得点は
(4+5)÷2=4.5(点) …(答)
であり、G子の最終得点は
4.5-1=3.5(点)
「3人の最終得点の平均は4点」なので、K子の最終得点は
4×3-(4.5+3.5)=4(点)
よって、1点以外の2回の得点の合計は
4×2=8(点)
2つの得点の合計が8点になる2回の点数は(3点,5点)しかないので
K子の3回の点数は低い方から順に1点,3点,5点 …(答)
解説を読めば簡単と感じたと思いますが、実際に解いてみるとJ子の点数が決まるところまで時間がかかったなんてこともあったことでしょう。
このような問題で何となく解けそうなのに決定打がなく、いたずらに時間を使ってしまうのが一番まずいので、試験本番では十分注意してください。
見切りをはやくし、解答順を間違えないようにすることが、本校の場合特に重要だということが本年度の問題でも確認できました。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
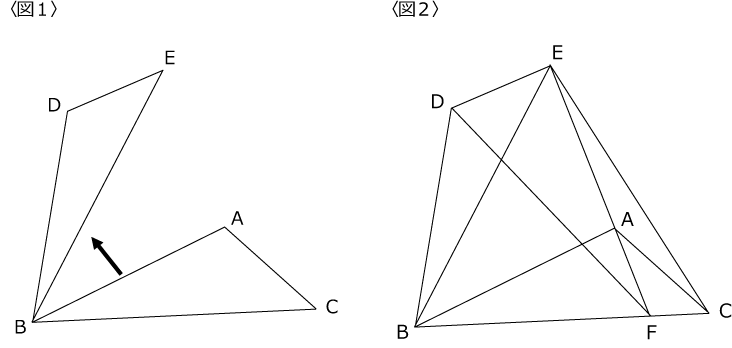
〈図1〉の三角形DBEは、∠ABC=20° の三角形ABCを点B中心に反時計まわりに回転したものです。
〈図2〉は〈図1〉のEからAに直線を引きBCとの交点をFとし、DとF、EとCを結んだものです。
また、BC=EC、∠BFD=50°です。
(1)∠EBAは何度ですか。
(2)∠DEBは何度ですか。
解答が表示されます














