VOL.2261問全力投球(9) 灘中
今年も既に入試が始まりました。
毎年注目している学校もあり、忙しくも楽しいのがこの時期です。
昨年から始めた「一問全力投球」として、最新の入試問題を紹介していきたいと思います。
まずはこのブログではお馴染みの「灘一日目」を取り上げたいと思います。
9の平面図形の問題を見てください。力試しに解いてみるのも良いでしょう。
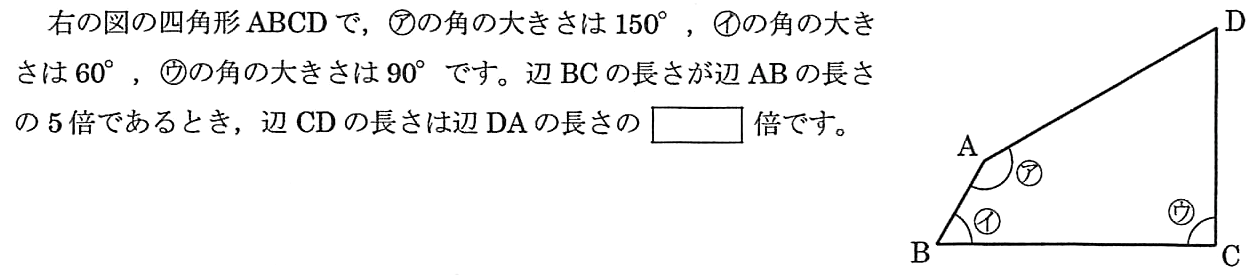
灘1日目の問題には毎年新鮮なテイストがありますが、対策で大切なのは過去問演習であることは言うまでもないでしょう。
この問題の答は5(倍)なのですが以下の作図で簡単に解けます。
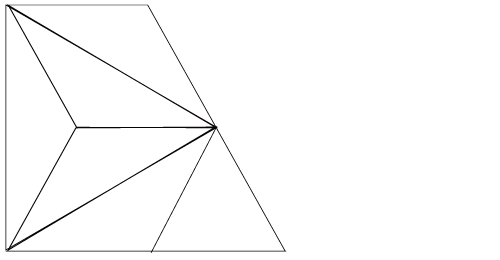
これを90度反時計回りに回転して左上を削り、右側を伸ばすと今年度の9になります。
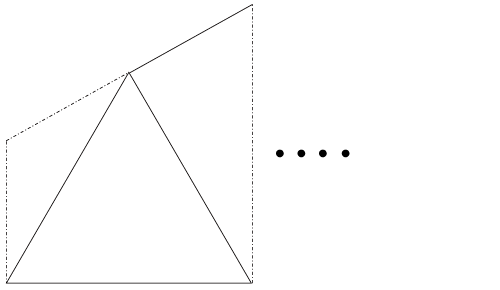
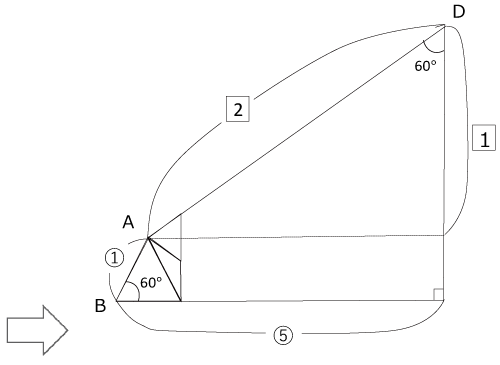
そしてこれを面積の等しい三角形に分割すると以下のようになります。
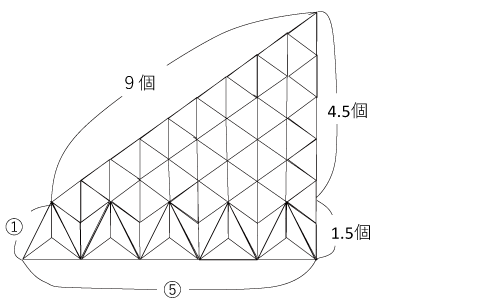
ここまでできればあとは三角形を数えるだけですね。
(9÷2+1.5)÷9= 2 3 (倍)…(答)
本問は過去問の重要性と図形的に処理することの大切さを教えてくれたと思います。
本校の合格を望むなら、本問のレベルは確実に正解できることを目指しましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題図形と角度
難易度★★☆☆☆
〈図1〉でPQは円Oの直径でRSとPQは平行、角ROSは90°です。
〈図2〉では直角二等辺三角形ABCの斜辺ACと三角形ACDの辺ACが重なっています。また、角CAD=22.5°、角ADC=45°で、AB=4cmです。
(1)〈図1〉の∠RQSは何度ですか?
(2)〈図2〉の三角形ACDの面積を求めて下さい。
〈図1〉

〈図2〉
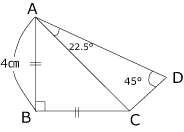
解答が表示されます