VOL.2271問全力投球(10) 開成中
今は情報化社会ですからスピードが大切だと思います。
今回、試験実施日2月1日の問題を取り上げるのも必然の流れなのかもしれません。
ということで、今年の開成中学3を取り上げたいと思います。
早速、問題をみてください。
さて、このブログでも「場合の数」は厄介な分野であると再三訴えてきましたが、本問の場合はどうだったのでしょうか。
結論から言うと、できれば完答したい問題だったと思います。
そのあたりを踏まえて解説していきます。
〈解説〉
(1) 「黒くぬりつぶすマス目は上下左右が隣り合わない」というのが、かなりきついしばりなので考えやすかったと思います。
縦方向のAとBを交互にすれば横の1~7は全て埋められますから
7か所・・・(答)
A始まりとB始まりがあるので
2種類・・・(答)
(2)
(ア) 5か所ぬりつぶすので1~7番のうちの5か所がぬられるわけです。つながっている部分に関しては2通りのぬり方があることを押さえておけば大丈夫です。
2番と4~7番の1かたまりがそれぞれ2通りずつあるので全部で
2×2=4(種類)
あります。
それを踏まえて解答欄に書き込みます。
(答)
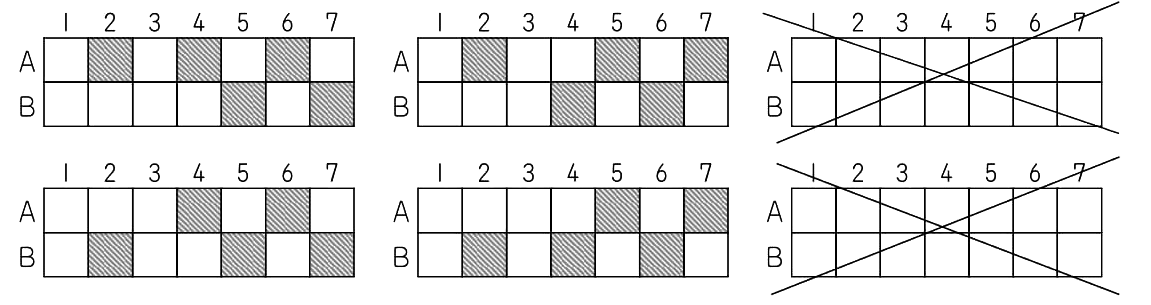
(イ)3列目と5列目をぬりつぶさないと3つにわかれるので
2×2×2=8(種類)
(ウ)まずはここが最初の山場です。
今までの誘導から場合分けするのはほぼ必然でしょう。
5個のものをいくつかに分けるのは仕切りを入れる例のやつでいけますから、見通しが立ったことでしょう。
かたまりごとに2通りずつあることに注意してそれぞれ求めていきます。
i)1かたまり
仕切りが左端に2個くっついている場合を(左端2)とあらわすことにすると、
(左端2)、(左端1,右端1),(右端2)の3通りあるので
1×3×2=6(種類)
ii)2かたまり
5個を2つに分けるのは仕切りの入れ方を考えれば4通りです。
仕切りが(左端1,内側1),(内側2),(内側1,右端1)の3通りあるので
4×3×2×2=48(種類)
iii)3かたまり
5個を3つに分けるのは4つの中から2つを選ぶ組み合わせなので
4×3÷(2×1)=6(種類)
です。
それぞれのかたまりごとに2通りずつあることから
6×2×2×2=48(種類)
以上をまとめて
6+48+48=102(種類)…(答)
(3)ここまできたらほぼ作業だけですね。
1マスもぬりつぶさないものに注意が必要なはずなのですが、解答欄の個数が6個しかないという親切仕様でした。
(ア)の答えは

ここで決めに行きましょう。
前の結果を利用するタイプなので表に整理します。
一つずつ付け足していくのですが、最後で分類します。
ぬりつぶし「無し」か「有り」ですが、「有り」は上と下があるので最初は2通りあります。
その先は前が上なら後ろは下という具合で一つに決まります。
・「無し」→前の「計」
・「有り」→前の「無し」×2+前の「有り」
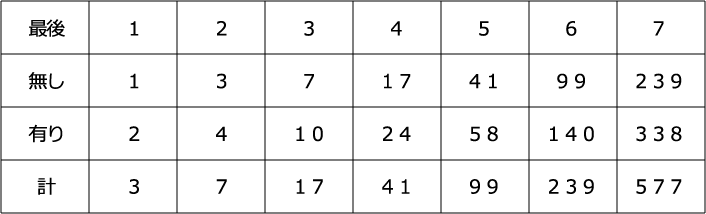
以上より、
(イ)17(種類) (ウ)577(種類)・・・(答)
いかがでしたでしょうか。
本ブログの読者なら頻出のテーマだったと感じたことと思います。
VOL.110、VOL.111で書いていた内容そのものみたいな問題でしたね。
仕切りを入れて解くことに関してはVOL.71で書いてます。
特にVOL.111の今週の1題の(1)を説く際の表は、本問よりもやや難しめだったと思います。
本ブログの内容が最難関校の問題に対応できていることを確認でき、気分が良い金田なのでありました。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。














