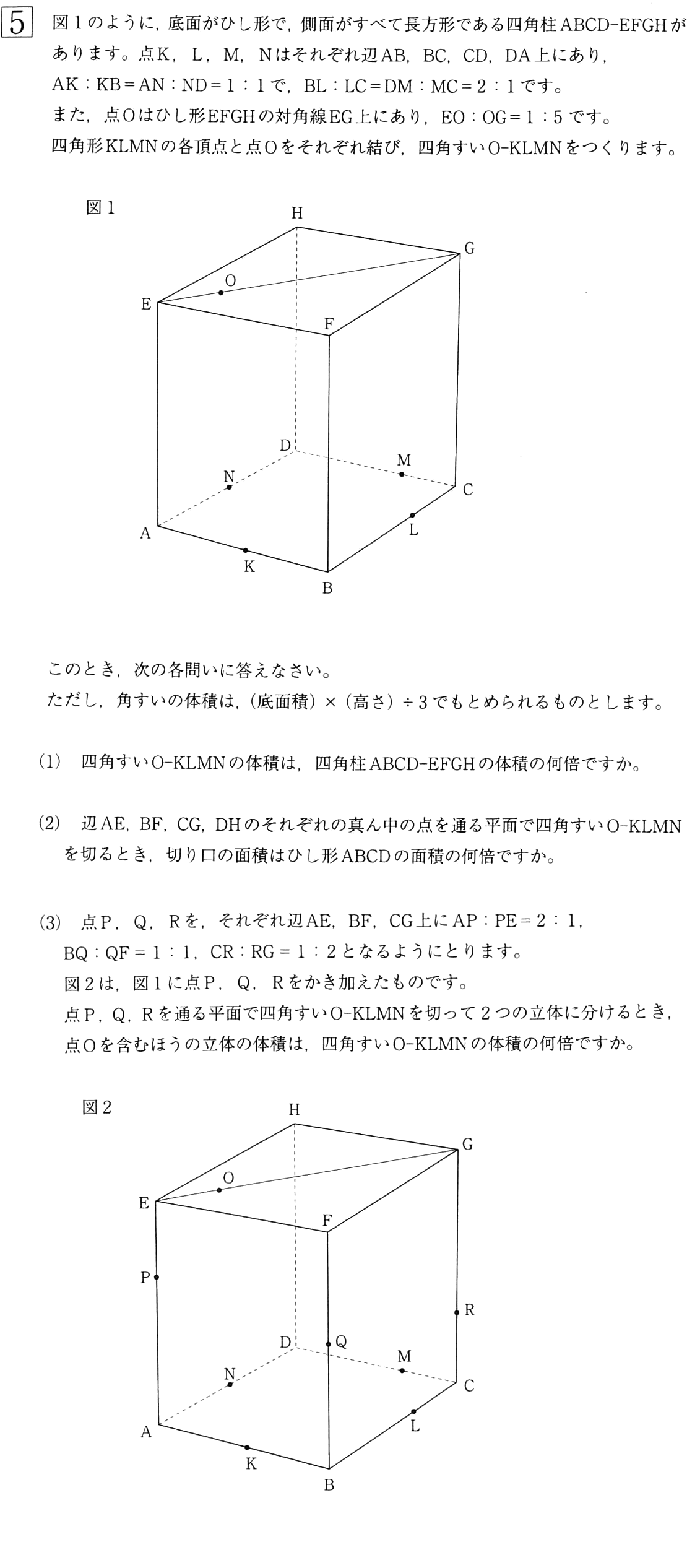
VOL.217１問全力投球（３）　渋谷教育学園幕張中

今回の「１問全力投球」は「渋谷教育学園幕張」の2021年度一次５を取り上げます。
問題を見てみましょう。

「立体の切断」の問題です。
本校では５が「立体切断枠」のようになっていますね。
ということで対策が必須です。

「立体の切断」は出題する学校とそうでない学校が割とはっきりしているので、出す学校を受けない場合は、厚い対策は不要だと思います。
立体切断は「柱体」と「すい体」に分類できます。
それぞれ公式があるので、しっかりと覚えておいてください。

最近の傾向としては「立方体」を複数の面で切るものが多かったイメージがありますが、本問は「すい体」の斜め切断でした。
「すい体」は「三角すい」が基本です。
「四角すい」以上は「三角すい」を組み合わせたものとみなします。

本問の場合、「斜め切断」は（３）でしたね。
（１）は「平面図形」、（２）も底面に平行な面で切るのでほぼ「平面図形」で片付きます。
それでは解説に入ります。

〈解説〉
（１）
ひし形は〈図１〉のように無条件で対角線を引いてかまいません。

〈図２〉は〈図１〉に四角形ＫＬＭＮを書き加えたものです。
四角形ＫＬＭＮは四角すいＯ-ＫＬＭＮの底面なので、四角形ＫＬＭＮの面積がひし形ＡＢＣＤの何倍かがわかれば、答を求めることができます。

四角形ＫＬＭＮは台形なので、ひし形ＡＢＣＤとの面積比べを考えます。
四角形ＫＬＭＮの上底と下底・高さが、ひし形ＡＢＣＤの対角線（縦・横）のそれぞれ何倍かを求め、それを掛け合わせたものが面積の割合となります。

（  １  ２  ＋  １  ３  ）×（  １  ２  ×  １  ２  ＋  １  ２  ×  ２  ３  ）＝  ３５  ７２  ・・・①

高さの等しいすい体と柱体の体積比は柱体を１とすると
「すい体の底面積の割合×  １  ３  」で求めることができるので

  ３５  ７２  ×  １  ３  ＝  ３５  ２１６  (倍)・・・(答)

（２）
四角すいを底面と平行な面で切っています。
高さの  １  ２  のところで切っていますので、その切り口は底面と相似で相似比は２：１です。

面積比は
２×２：１×１＝４：１
なので、①の  １  ４  倍が答です。

  ３５  ７２  ×  １  ４  ＝  ３５  ２８８  （倍）　…（答）

（３）
〈図３〉はＢとＤ、ＦとＨが重なって見える方向から見た図です。
「立体図形」はこのように平面的に捉えることが急所になります。
ＯＫとＰＲの交点をSとすると、ＯＳ：ＳＫを求めることが解決につながることがわかると思います。
ちなみに、図を見てわかるように、ＯＬとＰＲはＱで交わるのですが、これは対称性を考えれば明らかでしょう。

〈図４〉はＯＳ：ＳＫを求めるために「つの出し」を行ったものです。
ＥＧ＝１２
とすると
ＴＥ＝ＣＵ＝１２
ＥＯ＝２
ＫＣ＝９
なので
ＯＳ：ＳＫ
=１２+２：９+１２
＝２：３
であることがわかります。

ここで見取り図を〈図５〉で掲げておきます。

四角すいの体積比は、三角すいに分けて考える必要があります。
〈図６〉はＯＮＬの３点を通る平面で四角すいＯ－ＫＬＭＮを２つの三角すいに切り分けたものです。

三角形ＫＬＮと三角形ＬＭＮの面積比は台形ＫＬＭＮのＫＮとＬＭの比に等しいので３：２であることがわかります。

三角すいの体積の割合はＯから伸びている３つの辺の割合の積に等しいです（これは基本中の基本なので必ず身に着けておいてください）。
よって求める答は

  ３  ５  ×  ２  ５  ×  ２  ５  ×  １  ２  ＋  ２  ５  ×  ２  ５  ×  １  ２  ×  １  ２  
＝  １１  １２５  (倍)　　…（答）

以上見てきたように、基本の積み重ねできっちりと答を出すことができます。
そして、「立体図形攻略」に必要なことを教えてくれました。

上記のような「力」をしっかりと身に着けていきましょう。
そうすれば「立体図形」が得意分野に変わるかもしれませんよ。