VOL.2161問全力投球(2) 麻布中
今回の「1問全力投球」は麻布中2021年4をとりあげます。
解説を読んでいただければ分かると思いますが、分かってしまえば易しい問題です。
但し、その発想にたどり着けたかどうか。
個人的にはこのような「思いつくかどうか」というタイプの問題は好きです。
それでは問題を見ていただきましょう。
さて、この問題はどう解けばよいでしょうか。
「1.07」と「2.13」は足すと「3.2」なので、それを利用するやり方(芋づる算系)もありそうですが、今回は、「つるかめ算風」の解き方でやってみたいと思います。
〈解説〉
(1)
32枚全部カードAだとすると書かれた数の合計は
1.07×32=34.24
になります。小数部分だけ考えると、あと
0.78-0.24=0.54
増やせばよいことになります。
カードAとカードBを1枚入れ替えると
2.13-1.07=1.06
増えますが、小数部分に限れば「0.06」の増加です。よって
0.54÷0.06=9
の、9枚入れ替えれば良いことになります。その時の整数部分は
34+1×9=43…(答)
(2)
(1)と同じように考えます。
1.07×160=171.2
0.36-0.2=0.16
「0.16」は「0.06」では割り切れないので、整数を加えて割り切れるようにします。
3の倍数になるためには各位の和を3の倍数にすればよいので、「2、5、8…」(3で割って2余る数)を加えます。
(0.16+2)÷0.06=36
→171+36+2=209
(0.16+5)÷0.06=86
→171+86+5=262
(0.16+8)÷0.06=136
→171+136+8=315
(0.16+11)÷0.06=186 …160を越えてしまっているので不可
以上より
(答)209,262,315
この問題を解く際大切だったのは「つるかめ算」の解法の考え方です。
① もし、全部「つる」だったら
② 現実とのギャップ
③ 1入れ替えたらいくつ増えるか
④ ②を③で割れば「かめ」の数が求まる
以上を小数部分に当てはめれば解決したのですが、「面積図」を使って機械的に解くことしかやってこなかった受験生がこの発想にたどり着いたかどうかは不明です。
また、この問題を「不定方程式」のように捉えると(1)はともかくとして、(2)が大変だったと思います。
1つ見つければ良いのですが、それがなかなか見つからないということがあったかもしれません。
いかにも本校らしい、その場での柔軟な発想が求められた問題だったと思います。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題2進数
難易度★★★☆☆
名門君と目白君は所属する野球チームのコーチから問題を出されました。

コーチ:今、〈図1〉のように4×4のますの中に石が置いてあるよ。
これから名門君だけに「0~15」のうちのどれか1つの数字を知らせるよ。
名門君はマスの中の石を1つだけ取り除くかどこか1マスに石を置いて目白君にその数字が何かわかるようにして欲しい。
〈図1〉を見ることができるのは名門君だけで、目白君は名門君が動かした後しか見ることができないよ。(実際はこの時点では名門君も〈図1〉の配置はわかっていません。挑戦する時に初めて見ることができます。名門君だけが〈図1〉を見て石を動かし、その後目白君が石の配置だけをみて数字を当てなければいけません。)
すごく難しい問題だから二人でじっくり話し合ってから挑戦しに来てね。
名門君と目白君はどうしたらよいか全くわからず、家庭教師のK先生にヒントをもらいに行きました。
K:まず、マスに0~15の数字を入れよう。さらに、それを2進数で表してみよう。
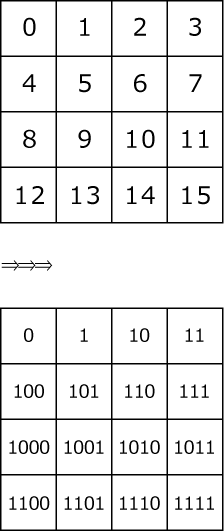
つぎに、2進数の「位」について見てみよう。
「1の位」「2の位」「4の位」「8の位」が出てきているよね。
それらがどこにあらわれているか調べてみるよ。
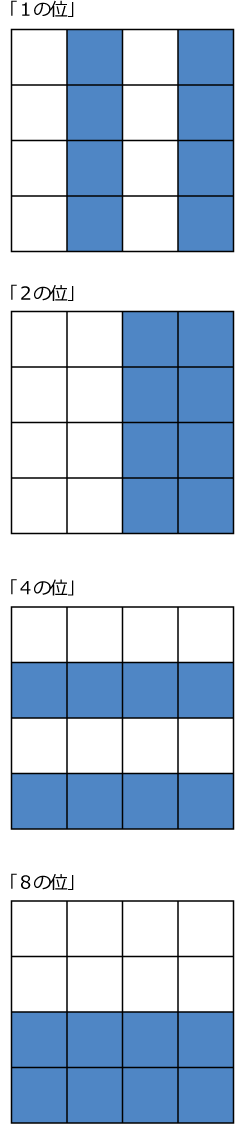
実はこれらを使えば、「0~15」の数字を1ヵ所のマスの石を増減するだけで表すことが出来るよ。
ヒントはたとえば「1の位」の色塗りの部分に石が奇数個ならば「1の位は1」、偶数個ならば「1の位は0」と決める・・・①
これを全ての位に適用すれば・・・。
K先生のヒントはここまででした。
名門君:K先生のヒントの①を適用すれば〈図2〉のように石が置かれていれば「1」を表すよね。

〈図3〉は「1の位」が2個、「2の位」が4個、「4の位」が2個、「8の位」が2個だから「0」をあらわしている!
この後、この数字の設定をそのまま使って、名門君と目白君はコーチに挑戦し見事勝利する事が出来ました。
(1)〈図1〉の状態だと「0~15」のどれをあらわしていますか。
(2)コーチの言った数字は「9」でした。名門君はどのようにして目白君に数字を伝えたでしょうか。
〈例〉のように答えてください。
〈例〉上から1番目、左から2番目の石を取り除いた。
〈例〉上から2番目、左から3番目に石を置いた。
解答が表示されます














