VOL.2181問全力投球(4) 筑波大学附属駒場中
今回の「1問全力投球」は「筑波大学附属駒場」の2021年度の[3]です。
さっそく問題をみてください。
今年は比較的点数が取りやすい問題が並んでいたのですが、[3]の(3)は満点の障害になっていたかもしれません。
「場合の数」は以前から言っているように点数を取りにくい分野です。
それと「立体図形」が組み合わされたのが(2)、(3)なので、間違えたとしてもそれは仕方なかったということでしょう。
ただ、うまい考え方ができれば正解できた可能性が高かったと思うので、それを紹介したいと思います。
〈解説〉
(1) 意外と条件を満たす線の引き方が少ないですね。
〈図1〉
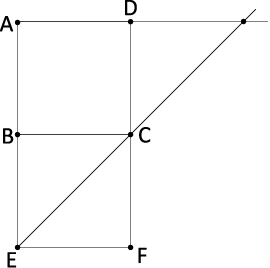
〈図1〉はA→Dを基準に、条件を満たす点を描いたものです。
この1つしかありません。
A→D以外にD→A、E→F、F→Eが同じことなので答は
1×4=4(通り) …(答)
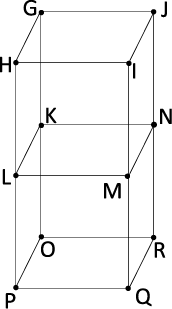
(2)〈図2〉のように頂点に名前をつけます。
当たり前ですが、2本の直線が通る点と交点は同一平面上にあります。
また、外側で直線が交わるためにはその平面上に少なくとも5点以上が存在するはずです。
そのような平面は底面OPQRと垂直な面に限られます。その面を真上からみたのが〈図3〉です。
6面あることがわかります。
〈図2〉
〈図3〉
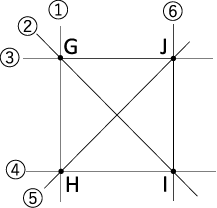
〈図4〉
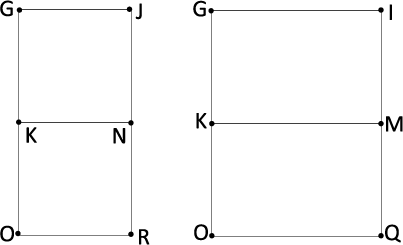
また、〈図4〉の2つの図形における条件を満たす交点は両方とも〈図1〉と同じです。
以上から
4×6=24(通り)
(2) いよいよ本題です。立方体がひとつ増えるとどのような影響があるのでしょうか。
こちらも平面の取り方は(2)と同じで、底面と垂直な面に限られます。
〈図5〉はそのうちの1つの面について調べたものです。
〈図5〉
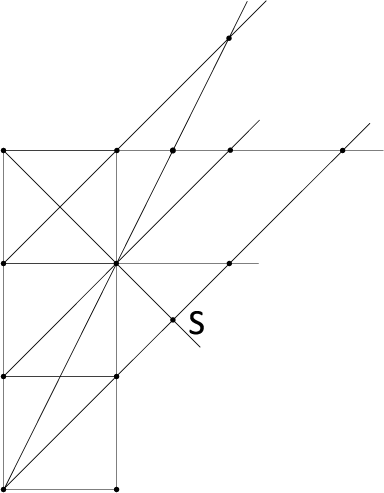
〈図5〉も4方向あるうちの1つを描いたものですが、ここから
6×4×6=144(通り)
とやってしまうと不正解になってしまいます。
点Sが右下と被っているのですね。
正解はダブりを調整して(一旦右側を求めそれを2倍)
(6×2-1)×2×6=132(通り)
いかがでしたでしょうか。
多分解説を読めばそんなに難しくないと感じたはずです。
問題は初見かつ自力でここまでたどりつけたかどうか。
やはり最終的には、算数の「力」に磨きをかけるしかないということになるでしょう。
・理論的に考える力
・作図力
・もれなく調べる力
これらをしっかりと鍛えていきましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題道順
難易度★★★☆☆
〈図1〉は12個の玉を20本の棒でつないだものです。
〈図1〉
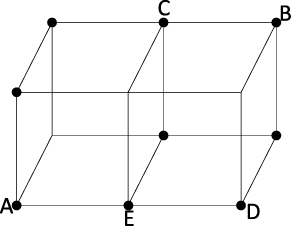
点Pは最初玉Aにあり、1秒ごとに棒で繋がれた隣の玉に自由に移動します。
例えば、2秒後に玉Dにいるためには、1秒後に玉Eに移動し、さらに1秒後に玉Dと移動する事になります。
(1)点Pが玉Aから玉Bまで最短の時間で移動する道順は、何通りありますか。
(2)点Pが5秒後に初めて玉Cに到達するような道順は何通りありますか。
解答が表示されます