VOL.192【入試問題を解いての感想2021】 -(6)灘 一日目-
前回は思い出に浸ってしまったので、今回はしっかりと算数の話をしたいと思います。
【入試問題を解いての感想2021】をやらなければいけません。今年は、様々な地域の学校にチャレンジしてみたいと考えています。今まで東京ばかりだったので、ここらで関西にいこうと思います。
本ブログでもお馴染みの灘1日目を今回は取り上げます。
毎年、新鮮な問題が登場するので、わくわくしながら解くことが多いのですが、今年はどうだったのでしょうか。
◎灘1日目
1素数が沢山出てくる計算問題
ある程度予想できていましたが、
2021=43×47
が出題されました。事前に知っていると少しだけ有利になりましたが、精神的なアドバンテージはそれ以上だったでしょう。
23つの容器に入った水の比から体積を求める問題
Bに入っていた水の体積を③とおくことが考えられます。
移した後のB:C=7:5
とすれば、関係式をつくることも容易だったでしょう。
3各位の和が5である4桁の数に関する問題
千の位で分類し、残りの3数の組み合わせを書き出すという要領で調べれば、特に問題なく正解できたと思います。
4正方形の辺上を3点が移動する問題
2つの出会いにかかる時間の比から、速さの比を求める問題でした。道のりの比も、2つの点の速さの比もわかっていたので、比の式さえ立てることができれば解けるという見通しが立ちましたね。
5A×Aが15で割ると1余るようなAの個数を求める問題
別の言葉に言い換えるのが良かったと思います。
・A×Aの一の位が「1」または「6」→Aの1の位「1」「4」「6」「9」
・Aが3で割り切れない
以上の2つを満たす2桁の数を求めれば良いことに気づけば、正解率が高かったと思います。
6約数すべてをかけあわせてできる数に関する問題
①はやってみれば良いので問題なかったと思います。
②は①を解く過程で本質に気づけるかどうかで変わってきたでしょう。
192=(2×2×2)×(2×2×2×3)
の後ろの(2×2×2×3)を2で割ったっものが答なのですが、なぜそうなるのかは考えてみてくださいね。
77倍すると4桁になり大きなものから順に並ぶ3桁の整数を求める問題
7の倍数の性質はあまり使うことはないと説明することが多いのですが本問では
・下3けたから千の位の数を引いたものが7の倍数
を使えば多少楽に解けたでしょう。2数が同じになるものがいくつかあるので、そこに引っかからないように注意が必要でした。本校に合格するような受験生なら大丈夫だったとは思いますが…
8長方形のまわりを正三角形が転がる問題
点Aが動いてできる線の長さはおうぎ形の弧を組み合わせたものです。正三角形が長方形のまわりを1周するだけなのですが、半径が3種類存在します。中心角も3パターンあるので、これらを手早くまとめる必要がありました。
9三角形を4分割した図形に1本線を引き交点がその線分を何対何に内分するかを求める問題
面積比を線分比に落とし込む問題でした。それを知っていれば問題なかったというレベルでしたね。
102つの三角形の重なりの面積を求める問題
2:1と4:3
の1と3の部分が共通という問題でした。高さが分かればあとは計算だけでした。
11水の入った三角すいの向きを変え水にぬれる部分を最小にする問題
側面の水にぬれている面積とぬれていない面積の比は変わらないので、その考え方を軸に解いていくことになります。
いかにも本校らしい、「大人の発想」が必要な問題で、差がついたとしたらここかなとも思いました。
12展開図から完成形の体積を求める問題
本校頻出の問題でした。これも毎度お馴染みなのですが、立方体から切り出した立体でしたね。さすがに見取り図は描いた方が良いでしょうが、それほど手間がかからない綺麗な問題でした。
以上みてきたように、極端な難問はほとんど無く、満点もいたと思われます。ミスが許されないという意味では厳しい試験だったかもしれません。
昨年にも増して高得点勝負になりました。本校の場合、高得点勝負になると差がつきやすくなるという傾向が見られるのですが、それは次のような理由と考えられます。
・過去5年間の受験者平均点の合格者平均点に対する割合は難易度に関係なく77~79%になっていた。
・ということは受験者平均点と合格者平均点の差は、合格者平均点の22%前後ということになる。
・よって合格者平均点の値が大きくなれば、差も大きくなる。
これを学校側がどのように考えるかですが、私にはわかりません。今後難易度がどうなるのか、興味が尽きません。個人的には皆をあっと驚かせるような新鮮な問題を出してくれることを期待しています。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★★★★
1辺が1cmの正三角形Aと1辺が1cmの正五角形Bがたくさんあります。
今、AとBを何枚かずつ使って下の条件1と2の両方を満たすへこみのない立体を作ることを考えます。
条件
1.AとBはそれぞれ少なくとも1枚は使う。
2.どの頂点についてもそのまわりが合同になっている(AとBの集まり方がどこも同じ。)
ぴったりと重なる立体は1種類とするとき、以下の問いに答えて下さい。
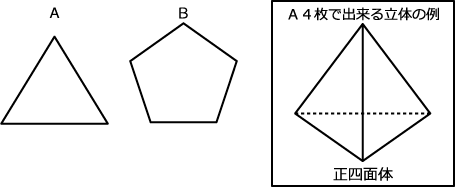
(1)Bを2枚使う時、Aは何枚使いますか?
(2)Bを12枚使う時、立体は何種類できますか? また、Aは何枚使いますか?全て答えてください。
解答が表示されます













