VOL.102【図形に強くなる】 -正確な作図(1)-
前回の「知識の充実」はいかがでしたでしょうか。
当たり前のことを言っているようですが非常に重要なので、もう一度確認をしておきます。
- 算数で大切なのは自分の頭で考えられるかどうか。
- 考えるためにはその“材料”が必要。
よって最低限の知識は頭に入れなければならない。 - その際、なぜそうなるのかを「理解」することが大切。
単なる丸暗記では使い物にならないし、定着率も悪い。 - 知識を身につける過程において、問題を正解するという成功体験から自信を獲得し、さらに論理的思考力も育まれれば理想的である。
- 学習の際、「覚えること」と「考えること」を意識し区別できるようになると、効率がよくなる。
- 以上は「図形」に限ったことではないが、「図形」は「センス」や「ひらめき」が必要と考えられているようなので、あえて「図形」における「知識の大切さ」を強調した。
少し内容を付け足してまとめてみました。参考にしてください。
今回は「正確な作図」についてテーマを絞って書いていきます。
「図形」に限らず「算数」において「作図」が重要なのは明白ですが、具体的にどうすれば良いかは以外と習っていなかったりします。
課題は人それぞれなので、集団授業では扱いにくい分野なのかもしれません。
線が真っ直ぐ引けなかったり、サイズが不適切等いろいろなパターンがあります。
できれば指導者に直接アドバイスしてもらいたいところです。
作図が得意な人は受験本番に近い環境(例えばA4の無地の紙→実際の問題用紙の余白と同じサイズ)で練習するのが良いと思いますが、あまり得意ではない受験生の場合は無地の紙に描くのは少し厳しい気がします。
一般的には方眼ノートを使っていることがほとんどでしょう。(実は私も愛用しています。このブログの問題も方眼ノートに手描きしたものから生まれているのです。)
ということで、方眼を利用した正確な作図を考えてみたいと思います。
まず、底辺と高さがわかっている三角形と平行四辺形はかなり正確に作図できると思います。底辺に対する頂点をどこにするかさえ気をつければかなり正確に描けますね。
正確に描きづらいものに「正三角形」があると思います。
もちろん、定規とコンパスを使えば「正三角形」の作図は可能ですが、今回は方眼を利用してフリーハンドでなるべく正確に描くことを考えてみます。
「正三角形」の高さは1辺の長さが決まれば自動的に決まるのですが、1辺の長さがわかった時点で高さは扱えない数字になってしまいます。
そこで、円周率と同様に近似値を利用することを考えます。
1辺が1cmの「正三角形」の高さはおよそ0.866cmです。
そこで、1辺の長さと高さの関係を表にまとめます。
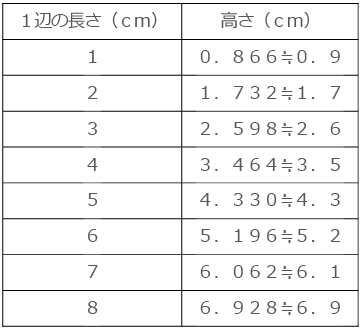
高さが整数になれば良かったのですが、あいにくこの表ではありませんでした。
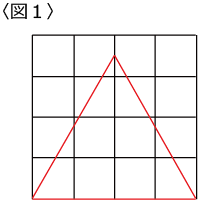
お勧めは1辺4に対して高さ3.5です。実際に描くと〈図1〉のようになります。
ほぼ正三角形に見えますね。
これを利用すると円もかなり正確に描けるようになります。
〈図2〉は正方形の内部に正三角形を2つ描いたものです。

Oを中心とする半径4の円は〈図2〉のA、B、C、Dを通るので〈図3〉の要領で四分円を作図することができます。
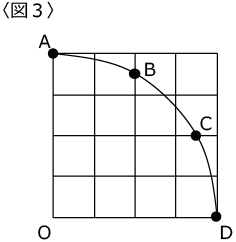
次に、少しマニアックかもしれませんが「正五角形」の作図について考えてみましょう。
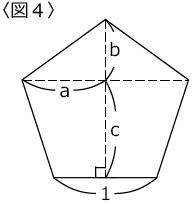
〈図4〉のようにa、b、cを定めます。
求め方についてはここではやりませんが(小学生の範囲ではありません)、近似値は次のようになります。
a=0.809
b=0.588
c=0.951
これをもとに表を作ります。今度は単位は無しにします。
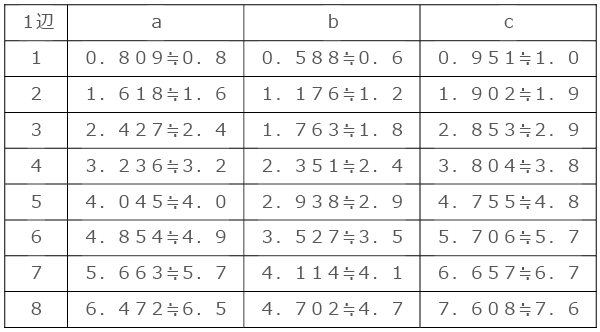
さて、少し悩ましいことになりました。
1辺の長さとcの長さがほとんど変わらないため、1辺が8までだと方眼半個分の差にもならないのです。
なのでどこかで妥協しなければなりません。
《案1》 簡易的な作図
1辺 … 3
a … 2.5
b … 2
c … 3
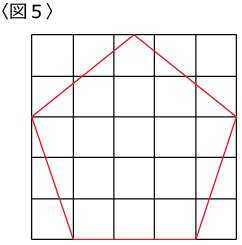
とします。
〈図5〉のようになります。
《案2》 正確さにこだわる
1辺 … 5
a … 4
b … 3
c … 4 3 4 (5としても良いでしょう)
〈図6〉のようになります。
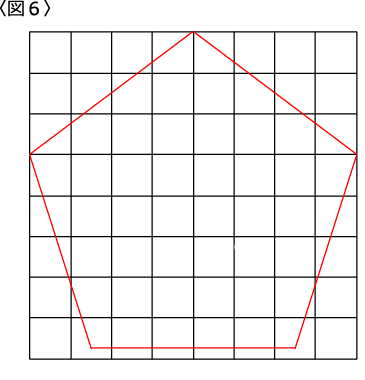
〈図5〉は少し縦長に見えますが〈図6〉はほぼ正五角形に見えると思います。
一度方眼ノートに描いて出来栄えを実感してみてください。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
〈図〉は1辺が18cmの正方形ABCDに円Oが内接している様子をあらわしています。
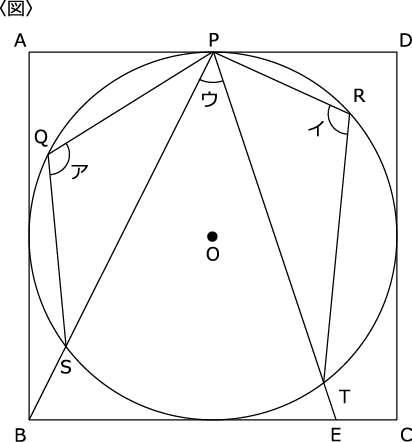
Pは正方形と円の接点、Q、R、S、Tは円周上の点、Eは直線PTと辺BCの交点です。
角アと角イの和が225°のとき以下の問に答えてください。
(1)角ウは何度ですか。
(2)BEは何cmですか。
解答が表示されます













