VOL.103【図形に強くなる】 -補助線-
前回の内容によって、正三角形や円、正五角形をかなり正確に描けるようになったと思います。
図形の問題を解くには「図形的感覚」が必要ですが、それを鍛えるのには実際に図形を描くのが有効です。
面倒くさがらずに、できるだけ正確に描くようにしましょう。
さて、今回は「補助線」についてです。
自称「図形が苦手」という人に、「図形が苦手な原因」を質問すると
「補助線をどう引いたら良いかわからない」
という返答を受けることがあります。
私はこの答を聞くと「なるほど」と思うと同時に、
「そりゃそうだろうな。根本がわかってないもんね。」
とも思ってしまいます。
なぜそのように思うかを説明します。
受験生なら誰もができなければならないようなレベルの有名な問題集の「平面図形」の問題を調べてみました。
36題のうち11題は補助線を必要とする問題でした。
さらに、少しレベルが上の問題集を調べたところ40題のうち13題は補助線を必要とする問題でした。
ということで大体3分の1程度の問題が補助線を必要とすると考えてよさそうです。
皆さんはこれを多いと感じますか。
それとも少ないと感じますか。
「図形が苦手」な人にとって、「補助線は引かなければならないもの」になっている可能性があります。
指導していて感じるのは、図形があまり得意でない生徒ほど補助線を引こうとする、ということです。
むやみやたらに線を引っ張っている感じです。
そんなことをしても当たるはずもなく、事態は悪化するばかりです。
補助線を引かなければならないのは3分の1程度です。
引かなくても解ける問題はそのまま解いたほうが効率が良いのです。
補助線を引く問題よりも引かなくても解ける問題の方が多いので、まずそちらを出来るようにしてください。
そうすれば、3分の2程度は正解できるようになる理屈です。
「補助線」はその後の話にしても良いぐらいです。
ですから、「図形」が苦手な原因を「補助線が引けないこと」だと思っている人は「根本」がわかっていないと感じてしまうのです。
さて、以上の話から問題に取り組む際の姿勢として
① 補助線は引かずに解けるかどうか考えてみる → 解法が浮かべばそのまま解く
↓ (補助線が必要な場合)
② どのような補助線が有効か考えてみる
↓ (補助線と解法はワンセット)
③ 補助線を引く(新たな図形ができる) → 解く
といった手順になることが考えられます。
ここで重要なのは、「形」と「解法」を結びつけてあるかどうかです。
これができていないと①の部分が厳しくなります。
漠然と「図形」を眺めていても「解法」が浮かぶはずもなく、勢い「補助にならない線」を大量に引っ張ることになります。
このことも
「解けない」 → 「補助線が引けない」
とつながっていくことを示しています。
本当の原因は「形と解法を結びつけていない」ことなのですが、当人にはその自覚がないのですね。
ここまで書いてきて話がVOL.101の「知識の充実」に戻っているのに気づきます。
今回それに加えるとしたら「形」をしっかりと意識するということでしょうか。
「補助線」を「引かない」ことについていろいろと書いてきましたが、ここからは「引く」方について書いていきます。
「補助線」をやたら描くことのデメリットは「当たることがほとんど無い上に、むしろ解くのに邪魔になる」ことなのですが、引いても損のない「線」もありますのでそれを紹介します。
無条件で引いてもよいもの
- ひし形の対角線
→ 合同な直角三角形が4個できる - 円の中心と円周上の点を結ぶ
→ 二等辺三角形や正三角形ができる - 正六角形を正三角形6個に分割
→ 面積比べの基準にしやすい
ほぼ得するもの
- 台形の対角線
→ 面積比が使える - 風車型の仕切り
→ 美しい形は良い形
求めるものによっては有力
- 垂線
→ 三角形・平行四辺形の高さを知りたい時・直角三角形の内部に引き相似を作りたい時 - 平行線
→ 角度を求める問題・三角形の相似を作るのに必須
そのほか「形を整えるために必要な線」として
- 延長線
- 対称軸
なども考えられるでしょう。
実際には上記の線を何本か組み合わせる必要があるケースもあるかとは思いますが、難易度が中程度の問題までならそれで十分対応できるでしょう。
これらの線は引いた状態で図を眺めればほぼ解けるたぐいのものばかりです。
なぜならば、それぞれの「補助線」には効果があり、それを知った上で線を引いているのですから、解けて当然です。
ということは、「補助線」は「解法」とほぼセットになっていなければならないということです。
「補助線」を引いたは良いが、その後も悩んでしまうというのは良くないのです。
悩むぐらいなら「補助線は引くな」です。
私はこのように考えています。
中学受験で扱われるテーマはある程度数に限りがあって、いくつかの「形」に分類されます。
実際の問題はその「形」とくらべて、線が何本か不足していることがあり、その分だけ難しくなっていると考えられます。
受験生サイドの考え方としては、その不足している線を埋めることを考え、それによって「知っている形」に持ち込むことが可能になります。
「形」をキチンと頭に入れ、なぜそうなるのかを理解したうえで結論を明確にしておけば、「足りない線」が埋められるとほぼ同時にその問題を解くことが可能です。
また、「損にならない線」を知っておけば正解率はさらに上がります。
普段からこのようなことを意識しながら「図形問題」に取り組むと、解ける問題の範囲がどんどんひろがっていくと思います。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
〈図1〉は∠A=∠D=30°の台形です。
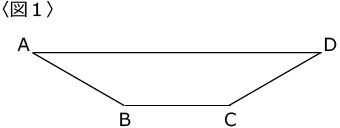
〈図2〉は∠E=∠H=105°で、面積が44cm2、EF=4cmの台形です。
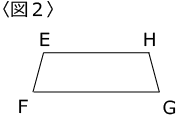
〈図3〉は〈図1〉の台形に、〈図2〉の台形と合同な図形3個を辺と辺でつないだ様子をあらわしています。

(1)〈図1〉の台形に外接する(点A、B、C、Dの全てが円周上にくる)円の半径を求めてください。
(2)〈図1〉の台形の面積を求めてください。
解答が表示されます













