VOL.101【図形に強くなる】 -知識の充実-
今回から、多くの受験生にとって、どうしたらできるようになるのか今ひとつピンと来ないと思われる「図形」について、私なりの考え方を書いていこうと思います。
第一回は、「知識の充実」です。
以前から何度も言っているのですが、「図形」は知らないとどうしようもありません。
逆に言えば知っていれば知っているほど有利です。
例えば、「公式」。
当然受験生の皆さんは知っていると思いますが、仮に知らないとすると「三角形の面積」を求めることすら危ういでしょうし、「円の面積」などはまず求めることができないでしょう。
これと同じようなことが、算数全般にも当てはまるのであるならば、なるべく多くの知識を頭に入れておくことが得策ということになるでしょう。
なぜ「図形分野」で「知識の充実」を強調するかというと、一般的に「図形分野」は「センス」や「ひらめき」が大切と考えられているふしがあるからです。
「図形問題は補助線一発で解決!」
というような見出しを見ると、そのような補助線が浮かばなくてはダメなような気になってしまいます。
そして、
「自分は補助線が浮かばないから図形のセンスがない」
とか
「ひらめかないのは頭が悪いせいだ」
というマイナス思考に陥ってしまいがちです。
これって、すごく損してると思うんです。
マイナス思考はとても厄介で、「算数」では「天敵」のようなものです。
「できない」と思い込んでしまうと、ほぼできなくなってしまいます。
「解けそうなイメージ」というのがかなり重要なのですね。
そして、この「解けそうなイメージ」の元になるのが「自信」です。
では、どうしたらこの「自信」を身につけることができるのでしょうか。
「自信」をつけるには「成功体験」の積み上げが有効と言われます。
「算数」で言えば「解けた」という経験を積み重ねることでしょうか。
このことは「算数」はできる側の人間はどんどんできるようになり、できない側の人間はいっこうにできるようにならないことを示している可能性があります。
実際そのような傾向があるような気がしますが・・・
整理すると、できる側にまわれれば特に問題はなく、できない側の人間はどうすればできるようになるか、そのきっかけをいかにして掴むかが重要ということになります。
まずは正解できるものを正解する、これが第一歩です。
そして、一番手っ取り早いのが「知っている」で解ける問題を正解することです。
実は「図形問題」はこの「知っている」を生かしやすい分野なのです。
例えば「角度」を求める問題は
- 三角形の内角の和は180°
- 平行線における同位角・錯角は等しい
- 相似な図形の対応する角は等しい
などの知識があれば解ける問題が多いでしょう。
特に、直接的に求められるものは最も簡単な部類に入ると思います。
「図形」が苦手な受験生が一定数いるのは、一工夫必要なケースで、何をどうしたらよいかわからないからだと思われます。
そしてこれを解決するのに「センス」や「ひらめき」が必要と考えられているのでしょう。
今回、言いたいのは、この「一工夫」の部分にある程度「知識」を取り入れていきましょうということなのです。
例えば、「三角形の内角の和は180°」という知識があれば「五角形の内角の和は540°」ということを導くことは容易でしょうし、「正五角形の1つの内角は108°」も求められます。
そしてこのあたりのことまでは「知識」にしている受験生も多いと思います。
確かに「N角形の内角の和」は「公式」があるのですが、実はここにヒントがあります。
この「公式」は「三角形の内角の和」をもとにしていますから、知らなくても何とかなります。
しかし、一々「三角形の内角の和」から出発すると面倒なのは明らかです。
「公式」って凄く便利ですよね。
前回書いた「公理」・「定義」→「定理」もこれと同じことです。
「知識の拡張」が正解できる範囲を広げることにつながることは理解していただけたと思います。
ここで注意してもらいたいことがあります。
何かを覚える際は「丸暗記」をせずに「なぜそうなるか」をきちんと理解するようにしてください。
つまり、きちんと理解ができていれば、「知識を充実させる」過程において、「理論の積み上げ」が伴うということです。
そしてその蓄積が「ひらめき」につながっていくのです。
「図形」は持って生まれた「センス」や天才的な「ひらめき」が必須のものではなく、「知識」を充実させる過程で獲得することができる「論理的思考力」によって攻略できる可能性が高いのです。
それではまとめます。
- 「算数」は暗記科目ではないと言われるが、最低限の「知識」は絶対に必要である。
「知識」を獲得すればその都度正解できる問題が増える。
これは「自信」をつける上で大きい。 - 「知識」でかたずけることができればそれ程楽なことはない。
「受験」という観点からは、なるべくその範囲を広げておいたほうが有利であることは明白。 - 「図形」は「センス」・「ひらめき」が必要と思われるが、それは先天的なものが全てではない。
「知識」を拡張する過程できちんと「理解」をすることで獲得できる可能性が高い。
受験生の皆さんは今すぐ「知識」を充実させて、「図形」を得意分野にしましょう。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
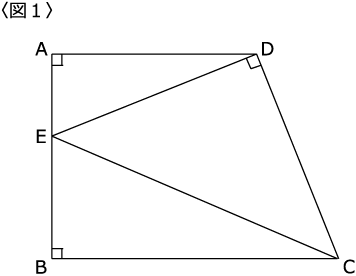
〈図1〉の台形ABCDの辺AB上に点Eをとると、
三角形DECは直角二等辺三角形になりました。
また、
AB=10cm
BC:EB=7:3
であることがわかっています。

〈図2〉は〈図1〉に、線分ECの中点をO、線分DCの中点をPとし、
Oを中心とした四分円とPを中心とする半円を加えたものです。
(1)BCの長さは何cmですか。
(2)〈図2〉の斜線部の面積は何cm2ですか。
解答が表示されます













