VOL.62点の移動(2)
私は見聞きしたことを算数と結び付けて考えるようなところがあります。
先日も成功の秘訣を聞かれたある経営者が「どれだけ本気になれるか」と答えていましたが、「算数ができるようになる秘訣にそのまま当てはまるなぁ」なんて考えていました。
よく受験生が本気になるのは最後の3ヶ月(特に男子)なんて言われますが、どう考えても今から本気でやった方が良いことは明白です。
大抵の場合、その時は本気のつもりだったが後から考えると全然なってなかったということなのですが、それでも良いと思います。
それこそが「成長」ということなのではないでしょうか。
そして、先ほどの経営者が「本気でやってもうまくいかないときはどうしたらよいか」と聞かれたときに「本気度が足りない」というようなことをおっしゃってました。
これまたそのまま当てはまります。
実はすごくシンプルで、「結果がでる=本気」ということなんだと思います。
「結果がでるまでとことんやる」という気持ちで頑張っていきましょう。
今回は最初に相談(VOL.53)に来ていただいたAさんに、その後の報告を兼ねて登場してもらいます。
Aさん本日もよろしくお願いします。
金田こちらこそよろしくお願いします。
その後、お子さんの成績はどうなっていますか。
Aさん以前とあまり変わらずブレが大きいように感じられます。
金田分数の計算はどうですか。
Aさんそれはかなり練習したので、間違えなくなりました。
金田それは素晴らしい。
そうやって課題をひとつひとつ克服していければ、どんどんできるようになるはずです。
Aさんただ成績はあまり変わっていないような気がするのですが…
金田算数の場合、勉強量と結果がすぐには結び付かないということがよくあります。
まして、塾のテストはいわゆる相対評価ですから、本人は前よりもできるようになっていてもまわりがよりできるようになっていれば成績は下がります。
テストは結果よりも内容を重視するようにしましょう。
成績が上がらなくても焦ってはいけません。
ある日突然飛躍することがほとんどなので、その日がくるまでじっと我慢です。
Aさんたしか、その期間の「プラスの声掛け」が大切だったんですよね。
私自身、それができているかどうか自信はありませんが、以前のように怒りにまかせて叱ることはしないようにしています。
金田それはとても良いことだと思います。
積極的に「プラスの声掛け」をしていただければそれが飛躍のきっかけになるかもしれませんよ。
Aさんはい、頑張ってみます。
金田今が一番辛い時かもしれませんが、不安定な成績が安定してくる時が来るはずなので、その時がくるのを待ちましょう。
ところで、Aさんから見て、今伸び悩んでいる一番の原因は何だと思いますか。
Aさん基本的な問題のミスもちょこちょこあるのですが、やはり難しい問題ができていないのが大きいと思います。
金田お子さんは「ニュートン算」や「動く図形」、「点の移動」などの分野はできていますか。
Aさんどれもあまりできていません。
金田これらは私が「上級分野」と呼んでいて(VOL.12参照)、そもそも複合的な内容になっている分野です。
当然、「基本」がしっかりしていないと歯が立たないことになります。
その中でも「点の移動」は「速さ」「図形」「規則性」などいろいろな要素が加わってくる可能性が高いので、厄介と言えるかもしれません。
Aさんどうすればよいのでしょうか。
金田そんなに心配しなくても大丈夫です。
基本からきちんとやっていけば十分攻略できます。
それでは「上級分野」への対応法を「点の移動」を例にとって説明しましょう。
まずは「速さ」の基本はしっかり身に着けるようにしてください。
特に「旅人算」「速さと比」「周回運動」あたりはきちんとやっておきましょう。
「周回運動」は「整数問題」や「規則性」が関係してくることがあるので慣れておかなければなりません。
また「グラフ」や「表」を書く必要があることもあるので、それらを「書く練習」も必要です。
ここまでしっかりやっておけばほぼカバーできると思いますが、中には「図形的要素」が強い問題もあるので、「図形(平面図形)」も基本を固めておかなければなりません。
また少し高級な問題を解くのに「シャドウ」や「相対速度」を使うケースもあるので、このあたりまで学習を深めることを目標としましょう。
Aさんやることが沢山あるんですね。
金田そうなんですが、そのほとんどが今までやってきたことです。
「点の移動」ができないということは、その前提となる基本的なことができていない可能性があるということを教えてくれているわけです。
良い「復習」の機会ととらえて、「基本」を固めてください。
そして、「基本」が完成すれば自ずと「応用問題」もできるようになるはずです。
Aさんわかりました。しばらくは、しっかり復習して足元を固めたいと思います。
<ポイント>
- 算数は「勉強量」がそのまま成績に結びつかないことがある。
そこで我慢して力をためることができれば、大きく飛躍できる可能性が高い。
「プラスの声掛け」を忘れずに。 - 「上級分野」は「基本」がしっかりしていないと対応が難しい。
- 「点の移動」は様々な分野が関係してくるので、「基本のチェック」という意味ではありがたい分野である。
「弱点」が見つかったらすぐに「復習」!
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題点の移動
点の移動の問題はVOL.12、VOL.36にもあります。
難易度★★★★☆
3つの円が〈図1〉のような位置にあります。
「円あ」は中心がOで半径が12cm、「円い」は中心がPで半径が3cm、
「円う」は中心がQで半径が3cmです。
点Sは「円あ」の周上にあり、3つの円は点Sで接しています。
〈図1〉の状態から、「円い」は「円あ」の外側をすべらないように接しながら、時計回りに1分で1周します。
同時に「円う」は「円あ」の内側をすべらないように接しながら、反時計回りに3分で1周します。
また、点Aは最初〈図1〉の点Sの位置にあり、「円い」が動き出すのと同時に
「円い」の周上を時計回りに1分で1周します。
さらに「点B」も最初〈図1〉の点Sの位置にあり、「円い」が動き出すのと同時に
「円う」の周上を反時計回りに1分40秒で1周します。
〈図2〉は「円い」、「円う」、点A、点Bが同時に動き出してから15秒後の様子を表しています。
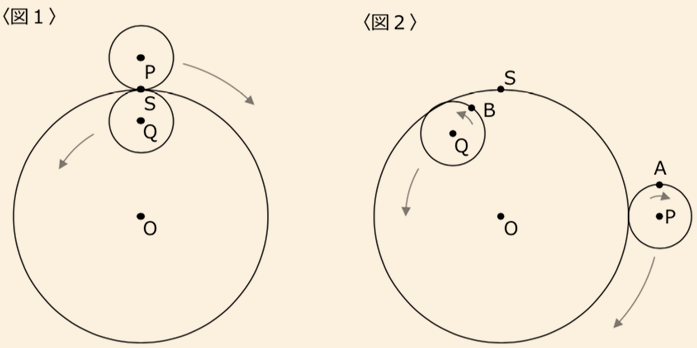
(1) 次のような状態に初めてなるのは、動き始めてから何秒後か答えなさい。
① A、P、Oの3点が同一直線上にある。
② P、O、Qの3点がこの順番に同一直線状にあり、かつ直線ABと直線PQが並行になる。
(2) 点Bが「円う」の周上を動く速さだけを変えて、6点O、P、Q、S、A、Bが同一直線状にくるのが最も早くなるようにしました。
点Bが「円う」を一周するのに何秒かかるように変えましたか。最も遅いものを答えてください。
解答が表示されます













