VOL.53「算数が苦手…」と言わないで!
今回から少し趣向を変えて、Q&A方式で算数についてみていきたいと思います。
母Aうちの子は算数が苦手です。
どのようにしたら苦手を克服できますか?
金田苦手といっても色々なケースがあります。
もう少し具体的に状況を教えていただけますか。
母A新6年生の男子です。4年生から塾に通っていて、成績は中の上ぐらいです。
算数だけがどうしても安定せず、テストで平均点を下回ることもしばしばです。
金田本人は算数に対して苦手意識を持っていますか。
母A本人はあまりそのようなことは気にしていないようです。
テストでひどい点数を取ってもいつもと変わらずのほほんとしています。
金田まず、言っておきたいのは、本人が苦手意識を持っていなければ、「苦手ではない」ということです。
算数はメンタルの占める割合が大きいので「苦手」と思ってしまうと点数が取れなくなってしまいます。
自分の実力を客観的に把握することは大切ですが、悲観的になることはマイナス面の方が大きいでしょう。
大切なのは試験当日点数が取れるというイメージを持つことです。
今は「根拠の無い自信」でもかまいません。
これからの頑張りでその「自信」を本物にすれば良いのです。
お母さんがあまりにも「苦手」を口にしていると、本当に「苦手」になってしまうことがあるので今後は「苦手」と口に出さない方が良いですよ。
母Aお話はなんとなくわかりましたが、テストで点数が取れないと不安になります。
成績を安定させるにはどうしたら良いのでしょうか。
金田ここでも誤解があると思うのですが、今の時期はそれほど「安定」にこだわる必要はありません。
私は成績が不安定な時こそ学力が伸びていると考えます。
不安定ということは悪いときもあれば良いときもあるということです。
毎回良いときの力を発揮できれば問題解決です。
大切なのはこの「成績が良いとき」を必ず拾ってあげることです。
「やっぱり、やればできるんだね。」というような声掛けを必ずするようにしてください。
そうすれば、自然とコンスタントに良い状態に近づいていきます。
母A私から見ると明らかに勉強量が不足しているように思います。
金田最適な勉強量というのは「目標に到達するのに必要な最低限の勉強量」と言い換えることができるでしょう。
難関校を志望するのであれば、「塾のテストで上位1割に入る」というように具体的に目標があるでしょうから、それに向けて計画的に取り組む必要があります。
ただし、勉強時間には限りがあるので、目標に到達しなくても切り上げなければならないこともあります。
このあたりの事情はケースバイケースなので、できれば指導者から指示を仰ぎたいところです。
単純な時間数の目安は平日6時間、休日10時間がMAXだと思います。
そのうち算数にあてる時間は、今の時期ならば全体の30~40%のケースが一般的でしょう。
もし息子さんが、上記の勉強量と比べ大幅に足りておらず、成績も振るわないのであればやはり勉強量が不足しているので、モチベーションアップの働きかけをする必要があるでしょう。
ただし、次のような流れは逆効果となるので絶対に避けてください。
「テストの点数が悪い」
↓
「叱られる」
↓
「強制的に勉強をさせられる」
↓
「モチベーションが上がっていないため勉強に身が入らない」
↓
「試験当日:勉強不足のためわからない問題が多い・叱られることを恐れ萎縮」
↓
「テストの点数が悪い」
↓
「また叱られる」
・
・
・
完全に「負のスパイラル」に陥っています。
プラスの声掛けが基本なので必ず実践してください。
同じ点数を取ったとしても、次のように持っていけるかもしれません。
「平均点は下回ったが先月よりも10点アップしていた」
↓
「10点もあがった!よく頑張ったね、という声掛け」
↓
「10点増えただけであれだけ褒めてもらえるならもっと頑張ってみようかな」
↓
「勉強量の増加」
↓
「試験当日:やったことがそのまま出た→これならいける!」
↓
「自己ベスト更新」
↓
「褒められる」
↓
「ますますやる気になる」
・
・
・
ちょっとしたことがその後の結果を大きく変えることがあります。
ときには「叱る」ことも必要だとは思いますが、感情的になって「怒りをぶつける」ことは何のプラスにもなりません。
絶対に避けるようにしてください。
母Aわかりました。これからは目先の成績にはこだわらず、プラスの声掛けを心掛けたいと思います。
<ポイント>
- 「苦手」は本人ではなく親が作っていることがほとんど。
- 成績が不安定なのは伸びている証拠。良い時を拾い上げる。
- 最適な勉強量は個々で異なる。勉強量を増やすためには本人のモチベーションアップが必須。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★★★☆
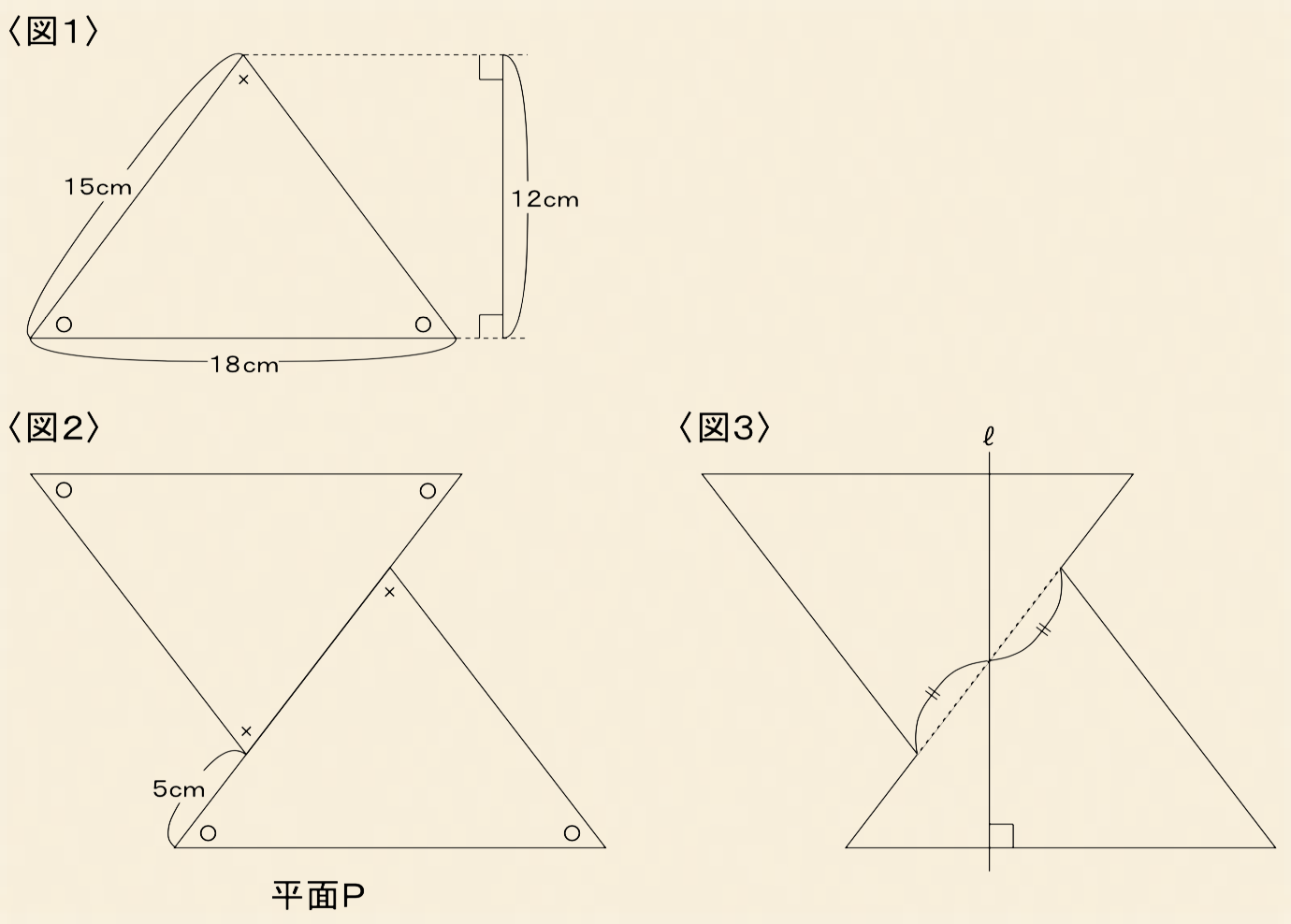
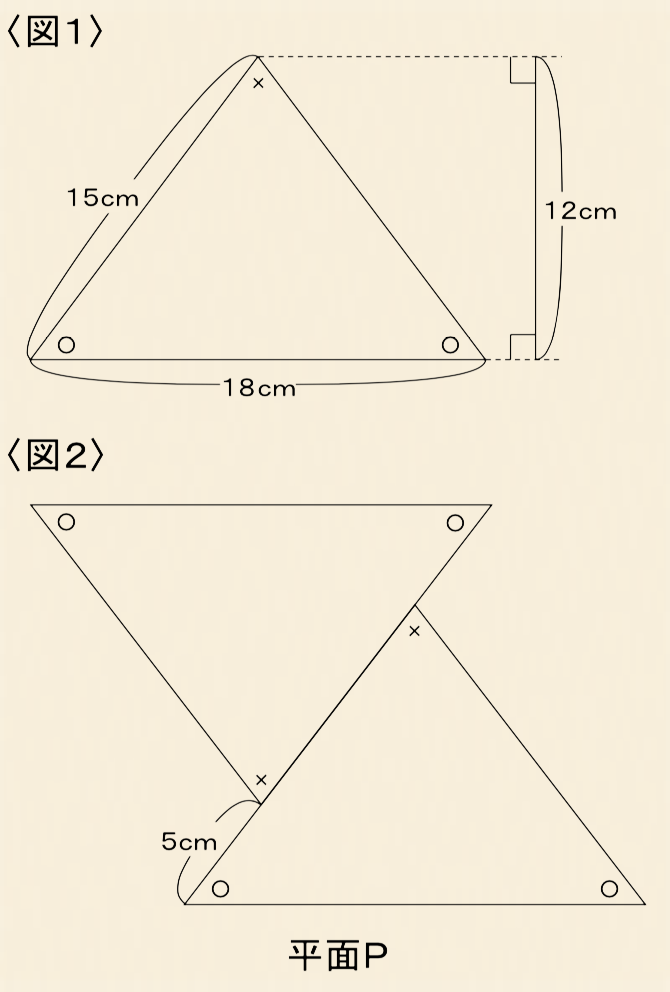
〈図1〉のような二等辺三角形があります。
これを2つ〈図2〉のようにくっつけて平面Pを作りました。
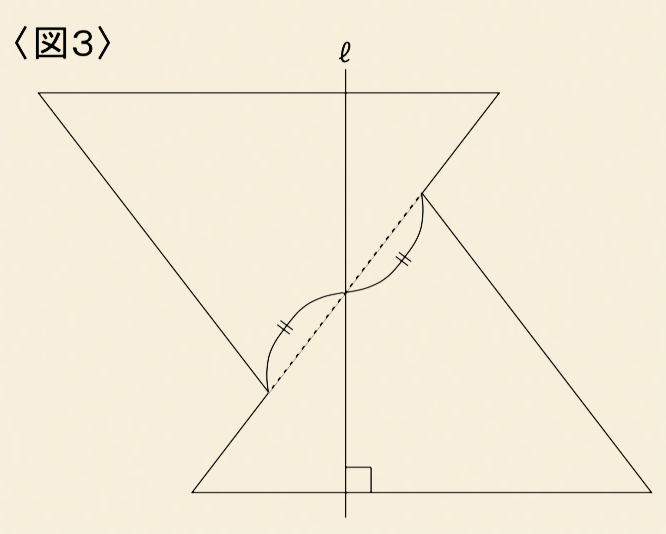
〈図3〉は平面Pと直線ℓの関係を表しています。
円周率を3.14とするとき、以下の問に答えてください。
(1)平面Pを、ℓを回転の軸として180°回転したとき、平面Pの通る範囲は立体になりますが、その表面積を求めてください。
(2)平面Pを、ℓを回転の軸として240°回転したとき、平面Pの通る範囲は立体になりますが、その体積を求めてください。
解答が表示されます













