VOL.61規則性
今、将棋ブームが到来しているようです。
私も将棋は好きなので、嬉しく思います。
また、将棋の上達法は算数に通じるところが多いので、参考にしています。
ブームを牽引している高校生棋士が快進撃を続けていますが、単純な脳内の処理のスピードでは、大人の棋士達を圧倒しているように感じられます。
彼は詰将棋選手権では小学生の時に日本一になっています。
年齢は関係ないというか、若ければ若いほど良いと思える程です。
個人差はあるかもしれませんが、受験生の皆さんの「脳力」自体は、大人とそれほど変わらないと思います。
不足しているものがあるとすれば、それは「経験」や「鍛錬」でしょう。
中学受験の良いところは自分を限界まで鍛えることができることだと思います。
どうせやるなら、楽しみながら、とことんやりましょう。
今回はVOL.58に来てもらったE君に再度登場してもらいます。
E君この間はありがとうございました。テストでは「図形問題」が解けました。すごく嬉しいです。
金田私もE君ができるようになって嬉しいですよ。
今日はどうしましたか。
E君「図形」はできるようになってきたのですが、「規則性」の問題でよく間違えるので、それを解決したいと思っておじゃましました。
金田なるほど、そうですか。
「規則性」にもいろいろありますが、順番にみていきましょう。
まず「植木算」。
植木を植える問題以外にもリングをつないだり、テープを作ったり、丸太を切ったり、とバリエーションが豊富です。
E君は「植木算」で何か気をつけていることはありますか。
E君特にありません。何となく習ったやり方で解くようにはしています。
金田習ったやり方を利用するのは良いことです。
それに加えて、気をつけるべきポイントを意識しておくと正解率が上がりますよ。
「植木算」の場合は「植木」の数と「間隔」の数の「ずれ」を意識することがポイントです。
「そんなことわかっているよ」と言うかもしれませんが、「植木」ではなく、「丸太を切る」ケースのように何か新しいものに置き換わると、すっかり忘れてしまうといったこともよくおきます。
「植木」以外のケースにも対応できるように普段から構えておきましょう。
続いて「方陣算」です。主に「中実方陣」と「中空方陣」に分類できます。
「中実方陣」は正方形になるので考えやすいと思いますが、「中空方陣」は仕切り方で解法が異なってきます。
E君はどんな仕切り方をしていますか。
E君僕は四隅に正方形をつくり、残りが長方形4つになるように仕切っています。
金田なるほど、それもなかなか良い仕切り方ですね。
ただ、私のお勧めは「4畳半」のような仕切り方です。
お互いに少しずつ譲り合うような形ですね。
見た目も美しく、このような仕切り方は大体「好形」になります。
では少しE君に描いてもらいましょうか。
思いついたものをいくつか描いてみてください。
―――E君は〈図1〉のように図形を3つ描いた。
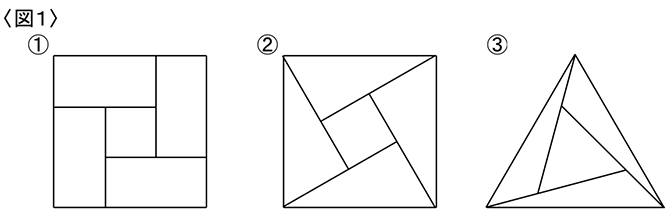
金田なかなか良いですよ。
それぞれが譲り合っていて実に平和です。
その他〈図2〉のような仕切り方もあるので参考にしてください。
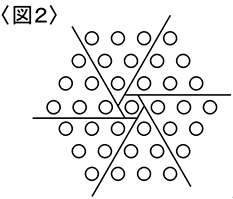
では次に「図形の規則性」にいきますね。これは様々なものがあるので、今回は「立方体の積み木」をピックアップします。
E君は「立方体の積み木」の問題を解く際、気をつけていることはありますか。
E君なるべく「見取り図」を描くようにしています。それを見ながら数えることが多いですが、よく間違えます。
金田残念ですが、「見取り図」を描くのはあまり得策ではありません。
現に間違えていることが多いようなので、そういった場合は他の解法を模索する必要があります。
「見取り図」があまり良くないのは、立方体の数が増えると描く手間がかかり過ぎることが挙げられます。
また、見えない部分が多いので、数えるのにも向いていません(特に数が増えたとき)。
ではどうすれば良いかですが、「数字に置き換えて処理する」のがおすすめです。
算数は「数量」⇔「図形」の変換が自由自在なら、本当に楽になります。
通常は「図形」で考えたほうが良いのですが、それだと面倒になる場合は逆に「数字」で考えるのです。
このことは非常に重要なので、いつも頭のどこかに入れておくようにしてください。
続いて「三角数」「四角数」にいきましょう。
E君は「三角数」と「四角数」が何かわかりますか。
E君「三角数」はわかるけど、「四角数」はわかんないや。
金田では「平方数」はわかりますか。
E君それはわかります。
金田「四角数」と「平方数」は同じです。
特に名前を覚える必要はありませんが、これぐらいは常識にしちゃいましょう。
「平方数」は同じ数字を2回掛け合わせたものですが、ある程度まで頭に入れておくと便利です。
E君はいくつまで覚えていますか。
E君13×13=169 です。
それより大きいのはちょっと…
金田17と19は素数なので、そこは覚えておいたほうが良いですよ。
16も2の累乗になるので重要度は高いです。
21×21=441 までは覚えておくのがお勧めです。
「三角数」は1から20位まで覚えておくと便利です。
とくに「19番目の三角数」は190で覚えやすいので必ず頭に入れておくようにしましょう。
最後に「数列」をみていきましょう。
「等差数列」「等比数列」「群数列」「分数列」等さまざまなものがありますが、一番の基本となるのは「等差数列」でしょう。
公式もありますから、取り組みやすいと思います。
E君は等差数列の公式は頭に入っていますか。
E君N番目の数は
「初項」+「公差」×(N-2)
だったかな?
あれ、「-2」か「-1」かわかんなくなっちゃいました。
金田正解は
「初項」+「公差」×(N-1)
でした。残念!
やはり、公式も理解を伴っていないと忘れてしまった時、どうしようもありません。
なぜ「-1」なのか真剣に考えてみることが大切なのです。
―――(E君はしばらく考えて)
E君そうか、N番目は1番目からみて(N-1)個先なので、「-1」なんだ!
金田そうです。そうやって自分の頭で考えれば印象にも残りますよね。
これで公式を忘れる可能性も少なくなりました。
今日は「規則性」のそれぞれの分野について考えてみました。
E君の頭の中が整理されていれば幸いです。
E君何かとてもすっきりした気分です。
すごくやる気がわいてきました。
今後もよろしくお願いします。
金田こちらこそよろしくお願いします。
<ポイント>
- 「植木の数と間隔の数のズレ」が「植木算」の急所。「植木」以外にもこの考え方を使えるように。
- 少しずつ譲り合うと「好形」となる(「好形」は応用範囲がひろい)。
- 公式は内容を理解した上でしっかり頭に入れる。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題規則性
規則性の問題はVOL.11、VOL.20、VOL.38、VOL.46にもあります。
難易度★★★★☆
下の図のような正四角すいPと正四面体Qが何個かずつあります。
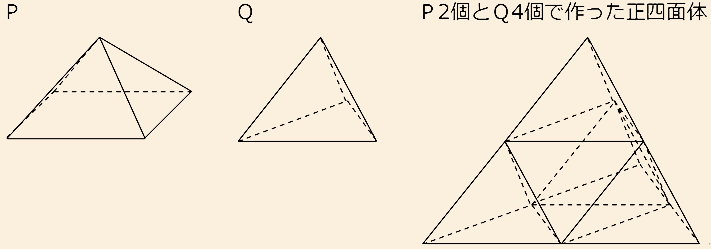
Pの底面は正方形、側面は正三角形で、その正三角形はQの面を構成する正三角形と合同です。
PとQを全て使い、中の詰まった正八面体をちょうど作ることができました。
また、PとQの個数の差は18個です。
(1) PとQはそれぞれ何個ずつありますか。
(2)PとQを使い、中の詰まった正四面体を作ります。いちばん大きなものを作るときPとQをそれぞれ何個ずつ使いますか。
解答が表示されます













