VOL.11数列
皆さん、勉強は順調でしょうか。
日に日に暑くなってきました。体調管理には十分注意して下さい。
さて、前回の問題(ブログvol.11<5/19号>)はいかがでしたか?
もし、(1)で6通りと答えて間違えてしまった人は要注意です。
うっかりかもしれませんが、その場合でも、「こんな簡単なこと聞くのかな?」という疑問は浮かぶでしょう。
そこで、振り返れれば間違いに気付く可能性があります。
今までの問題を解いていれば、(1)もそんなに楽ではないという感触は掴んでいると思うので、「6通り」に違和感を感じて欲しいのです。
このことは、入試問題にも当てはまります。
過去問を解いていくとその学校の問題の難易度の範囲が大体決まっていることに気付くでしょう。
難易度だけでなく、答が整数になることが多い、誘導が丁寧である等ある程度決まった傾向があることがほとんんどです。
これらは絶対ではありませんが、大きなヒントになる情報です。
例えば、毎年最初の計算問題が「1」や「2」というシンプルな答なのに、自分の計算結果が分母の桁が大きい分数になったならば、かなり怪しいと判断すべきでしょう。
状況にもよりますが、機械的な処理に走るのではなく、自分の頭で考えることを大切にしてください。
考えるということは、まず視野を広く持ち、その先の深いところを見ようとする努力から始まります。
日頃の勉強の姿勢が大切ということですね。
さて、今回のテーマは規則性です。
この分野特有の注意して欲しいことが二つあります。
一つは、「書き出しが基本だがそれに満足しない」こと。
もう一つは、「少しズレている間はまだ基本が完成していない」ということです。
塾のテストでは、100個ほど書き出して正解すればそれはそれで良いことになります。
しかし、実際の入試では1000以上先を求めなければいけないケースも多いので、書き出しだけでは正解できない可能性もあります。
学習の際は大きな数にも対応できる解法を身につけておきましょう。
規則性の学習を進めていくと、「当たらずとも遠からず」という時期があることが多いです。
実はここが正念場です。
自分なりの工夫で百発百中に持っていけるか、運任せのままなのかの瀬戸際なのです。
「1ズレた、惜しい!」ではなく、1ズレないようにするために自分は何をすれば良いのかを考えてください。
私からのアドバイスとしては、「書き出し」をうまく利用すること、「知識」を充実させておくことを挙げておきます。
「書き出し」についてはそれに頼るなと言ったばかりなので、矛盾していると感じるかもしれませんが、全部書けといってるのではありません。
具体例としては、最後のいくつかを「書き出し」で確かめたり、小さな数で実験するときに「書き出し」たりすることが考えられます。
「知識」に関しては『三角数』『四角数』を覚えておくのは常識でしょうし、さらに進んで『フィボナッチ数列』『パスカルの三角形』『継子立て』等を「知識」にしておけばかなりの安心感があります。
規則性は安定するまでは時間がかかるかもしれませんが、基本が完成すれば得点源として計算できます。
粘り強く取り組みましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題数列
難易度★★★★☆
下のように、分数がある規則にしたがって並んでいます。
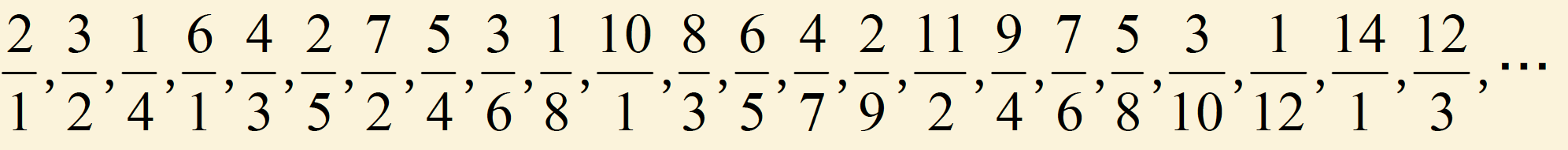
(1)200番目の分数はいくつですか。
(2)1番目からN番目までの全ての分数をかけ合わせた値が
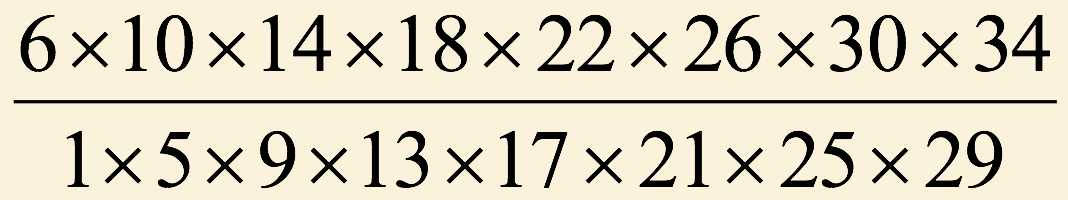
と等しくなりました。 Nを求めてください。
解答が表示されます
2120
(2) 152












