VOL.12点の移動
受験で大切なことに、「規則正しい生活」があります。
これは体調管理の基本であり、勉強時間の確保という意味でも、習慣化は大切です。
「規則正しい生活」が前回扱った「規則性」のマスターにつながるといえるでしょう。
ということで、前回(ブログvol.11<5/26号>)の問題を振り返ってみましょう。
オリジナリティーを出したかったので少し複雑な規則になってしまいました。
グループ分けに気付かないとどうしようもありませんが、(1)はよくある三角数の問題とあまり変わりません。
(2)もある程度書き出していけば、意味不明のまま終わるということはなかったでしょうし、書き出しの基本である「小さな数で実験して規則性を掴む」ということができれば、正解できたことでしょう。
では、どういう規則なのか全くわからなかった人はどうすればよいのでしょうか?
- 全体の流れを見る ⇒ 三角数・平方数
- ひとつ前と比べてどうなっているのかを調べる ⇒ 等差数列・階差数列・前の結果の利用
- 分数列の場合 ⇒ 分母と分子を別々に見る・分母と分子の和(差)を確認する・約分の有無
- グループ分けをする ⇒ グループに番号を振っておくと便利
以上をヒントとして挙げておきますので、問題を解くことによって規則性を見抜く力を養ってください。
予想 → 書き出し → 検証という手順を根気よく繰り返せば力は付きます。
「この数列はこういう規則性を持っています」という説明を聞いても、自分で見つける力はあまりつきません。
やった問題の復習も、記憶の定着という意味では良いのですが、見つける力の養成には向いていません。
以前も書きましたが、初見の問題に全力で取り組み、自分で見つけられるように努力するのが一番だと思います。
取り組む姿勢も「規則正しく」いつもブレないということが大切です。
今回取り上げる分野は『点の移動』です。
基本的には「速さ」の問題ですが、そこに図形的要素が加わるのがミソです。
さらに、「整数問題」や「規則性」の要素を持つ問題もあります。
私はこのように+αがある分野のことを「上級分野」と呼んでいて、難問が出やすいという認識を持っています。
上級分野は学習が一定以上進んでいないと点数が取ないことが考えられますので、集中力を高めて取り組みましょう。
ワンポイントアドバイスを以下に掲げます。
- 点の移動と面積の変化…移動する方向が変われば、面積の増減の仕方も変化します。範囲を明確にしましょう。
- 2点が周上をまわる…何周もする場合は規則性の問題になることが多いです。同一の辺上にくるケースは丁寧に調べる必要があります。
- 2点の移動…旅人算が使えないか検討します。段違いの出会いが典型例です。追い越しになるケースもあります。面積が関係する問題は比が使えるとわかり易くなります。
- シャドー…高級な考え方ですが、平均や相似を理解していれば大丈夫です。経験が大事なのである程度量をこなしましょう。
このように問題によっては色々な分野の要素が入ってきます。
グラフを書いたり、表をつくったりすることを求められることもあります。
苦手分野があるとそこに足を引っ張られてしまうので、これを機会に苦手は解消しましょう。
『点の移動』の問題を解くことは、算数の総合力を養うのに最適です。
色々な「力」が同時に鍛えられる「お得な分野」と考えるようにして、積極的に取り組みましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題点の移動
難易度★★★★☆
(図1)のようにたて30cm、よこ68cmの長方形ABCDがあります。
辺AB、BC、CD、DA上にそれぞれ点E、H、F,Gがあり、AE=DF=10cm、
AG=8cm、BH=26cmです。
点P、Q、Rはそれぞれ点G、F、Hを同時に動き始め、点Pは直線GD上を毎分6cmの速さでG→D→Gと1往復し、点Qは直線FE上を毎分13cmの速さでF→E→Fと1往復し、点Rは直線HC上を毎分3cmの速さでHからCまで動きます。
以下の問いについて、動き始めてからの時間を答えてください。
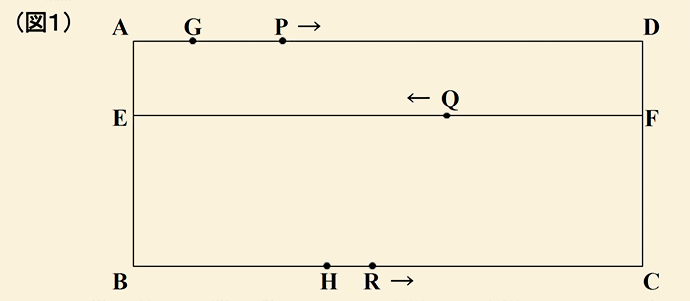
(1)台形PQFDと台形EBRQの面積の比がはじめて1:2になるのは何分後ですか。
(2)3点PQRがはじめて1直線上にならぶのは何分後ですか。また2回目に1直線上にならぶのは何分何秒後ですか。
解答が表示されます













