VOL.10色ぬり
おかげさまで、このブログも10回目を迎えることができました。ありがとうございます。
今までいろいろなことを書いてきましたが、ここで一旦まとめてみたいと思います。
『算数ができるようになる勉強法』
- 算数はどれだけ考えることができるかが大切なので、日ごろから自分の頭で考えることを大切にします。
- ただし、最初から全て自分で考える必要があるわけではありません。基本的な部分は十分理解した上で知識とします。その知識は通常自分で編み出すのはかなり困難(例えばつるかめ算の解法を自分で思いつくのは至難の業)なので、習えば良いです。
- 習う際は「なぜそうなるのか」をきちんと理解しながら進めましょう。
- 理解するとなんとなく覚えたような気になりますが、それでは不十分なことも多いでしょう。問題を解くことによって知識の定着を確実なものにします。
- 基本的な知識が定着したところで、応用問題を解くと良いでしょう。応用問題は細分化してその全てのパターンを記憶するような勉強法では限界がくる(ほぼ無限にパターンが存在するため)ので、基本的にはその都度自分の頭で考えて解くべきです。
- 自分の頭で考えることによって算数の『力』がつきます。この『力』こそが入試当日最も頼りになるものです。算数の入試対策はこの『力』を志望校合格レベルまで伸ばしておくことに尽きると思います。
- 考えるときは頭の中だけでなく、手を動かしながら(書きながら)考えましょう。その際適正なサイズで見やすく書くことを心掛けてください。
- 高級な知識を身に着けることはワンランク上を目指すのであるならば必須でしょう。高級な知識でライバルに差をつけましょう。
いままで書いてきたことをまとめると、以上のようになります。
手元にある教材を上手く使用して算数の『力』を大いに伸ばしてください。
今回のテーマは『場合の数』です。
まずは基本的なことからチェックしてみてください。
①順列と組み合わせの区別がつくか
②和の法則と積の法則の区別がつくか
①に関しては、高校生でもわからなかったりするようですが、具体例とともに頭に入れておけばそんなに難しいことでもないでしょう。
簡単にいえば、順番が関係あるのが順列で、関係ないのが組み合わせです。
②に関しては、場合分けをした(両立しない)ときは和の法則、おのおのにつき同じようにある(両立する)ときは積の法則と覚えておけば良いでしょう。
どちらにしても、区別がはっきりついて絶対に間違えないレベルにしておかなければなりません。
「順列・組み合わせ」は計算で解けるようにしましょう。
基本的には「樹形図などをかく」、「法則に気付く」、「計算でいけるところは計算」、「書き出して確認」といった流れが理想ですが、順列・組み合わせが明らかならば公式を使ってサッと計算で済ませましょう。
基本をクリアしたあとはなるべく多くの問題を解いて経験を積んでください。
多くの場合習った解法が使えるはずです。
そのことに自分で気づくこと、それが算数の力がついてきたことの証です。
場合の数は高級な知識の宝庫です。
また、検算が難しいため、複数の解法を習得することのメリットが大きい分野でもあります。
なので、他の分野よりも積極的に高級な知識にチャレンジするのも良いでしょう。
ただし、それは基本が完成した後の話です。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題色ぬり
難易度★★★★☆
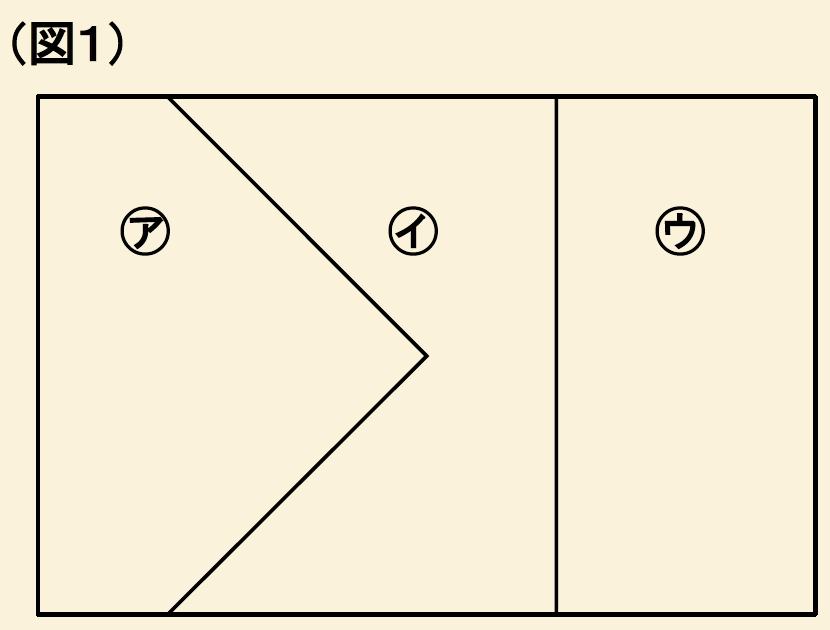
赤、青、黄、白4種類の絵の具が3gずつあり、(図1)の㋐、㋑、㋒をぬりわけます。
同じ色を2回使っても良いですが、となり合う部分は異なる色とすることにします。
㋐、㋑、㋒は1か所塗るのにそれぞれ2gずつ絵の具が必要で、全部塗るには合計6gの絵の具が必要です。
また2種類の絵の具を混ぜ合わせて使うこともできますが、その場合は必ず1gずつ合計2gを混ぜるものとします。
(1)赤2g、青2g、黄2gを使うとすると何通りのぬり分け方がありますか。
(2)全部で何通りのぬり分け方がありますか。
解答が表示されます













