VOL.56「立体を平面的に捉える」
世の中結果が全てではないと思いますが、勝負の世界では特に結果が重要視されるようです。
結果を出せば「大絶賛」、しかし結果がでなければ「解任」なんてこともあります。
受験でも結果が残せるように頑張っていきましょう。
今回はK市の小6女子のお母さん、Dさんからの相談です。
Dさんうちの子は「立体図形」が苦手です。やはり「立体図形」は男子より女子のほうが苦手としているのでしょうか。
金田 脳の機能が男女で差があるのかどうかは、まだわかっていないことも多いと思います。
「空間把握能力は男子のほうが優れている」という意見もあるようですが、たとえそうだとしても「中学受験」ではあまり影響ないと考えています。
受験では能力そのものよりも、自分なりに準備をしておくことが大切でしょう。
何となく女子のほうが「立体図形」が苦手というイメージがありますが、これは女子のほうが自己評価が厳しく、やや悲観的なことが原因なのかもしれません。
私が実際に指導してきた経験では、男女による差というのはほとんど無いですよ。
Dさんそれを聞いて少し安心しました。
ただ、娘が「立体図形」があまりできないというのも事実です。
どうしたらよいのでしょうか。
金田 まず「立体図形」は、「平面図形」という土台がしっかりしていないといけません。
「平面図形」はできないけれど「立体図形」はよくできる、ということは通常はありませんし、まず間違いなく「立体図形」もできないということになります。
ですから順番としては
①「平面図形」→ ②「立体図形」
というように課題を克服していく必要があります。
娘さんは「平面図形」はできていますか。
Dさんものすごく得意というわけではないですが、塾のテストでは平均点以上の点数は取れています。
ところが「立体図形」になると平均点に満たないことがほとんどです。
金田 そうなりますと「立体図形」の問題を解く際に必要な「あること」が身についていない可能性が高いですね。
Dさんえっ、その「あること」って何ですか。
金田 それは「立体を平面的に捉える」ことです。
Dさんそれは聞いたことがあります。ただ、具体的にどういうことかはよくわかりません。
金田 現状では「立体図形」の問題も紙の上で出題されているので、「平面」に置き換えられているわけです。
具体的には「見取り図」「投影図」「展開図」のどれかが使われることが多いです。
つまり、大半の問題は与えられた時点で「平面」に置き換えられているので、それをそのまま利用できれば特に問題はないということになります。
実際は「見取り図」が平面としての意味があまりないため、別の捉え方をする必要があるケースが多いです。
また「展開図」は使えるケースが限定的で、一旦、頭の中で組み立てなければならないこともあります。
「投影図」が「平面的に捉える」という趣旨には一番合っていますが、方向を変える必要があることも多いです。
Dさん何となくわかりましたが、やっぱりちょっと難しいです。
金田算数でよくやることなのですが、よくわからない時は「別のものに置き換える」という
ことが急所になります。
イメージとしては次のような変換が行われると思ってください。
「平面」→「立体」→「平面」
最初の変換は問題が何を言っているのかを捉えるのに必要で、2回目の変換は解くために必要ということです。
このあたりのことが丁寧にできるかどうかで結果が変わってくるような気がします。
「立体図形」の問題の難易度は、それぞれの変換の難易度によるところが大きいと思います。
Dさんどういう練習が効果的なのでしょうか。
金田 「図形」は「描く」ことが基本なので、まずはそれぞれの図をきちんと描けるように練習してください。
「平面的に捉える」という点については、形によって「都合の良い向き」というのがある程度決まっているのでそれを頭に入れておくと良いです。
そしてその「都合の良い向き」から見た「投影図」等を「描く」練習をするのです。
Dさんなるほど、良くわかりました。早速「描く」練習を始めたいと思います。
<ポイント>
- 女子だからといって「立体図形」を必要以上に恐れる必要はない。
- まずは「平面図形」を得意分野にする。
- 「平面的に捉える」ことが急所。描くことと合わせてしっかり練習しよう。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題展開図
難易度★★☆☆☆
「水」の問題はVol.6にもあります。
〈図1〉はある立体の展開図です。
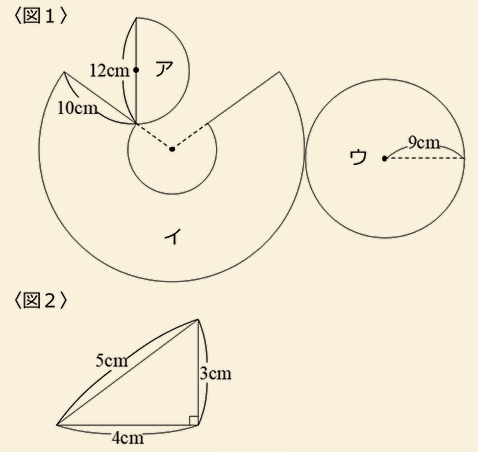
アは半円、イは中心が同じである大きなおうぎ形から小さなおうぎ形を取り除いた形、ウは円です。
円周率を3.14として以下の問に答えてください。
(1)この立体の表面積を求めてください。
(2)展開図が〈図1〉のようになる立体は2種類考えられますが、その2つの体積の和は何cm3になりますか。 ただし、〈図2〉のように3辺が3cm、4cm、5cmの三角形は直角三角形です。
解答が表示されます













