VOL.50平面図形
3月に入りました。
まだ、寒い日もあると思います。体調管理には十分注意してください。
今回は前回書けなかった女子校・共学校の入試問題について、私の感想を書きたいと思います。
まず感じたのが、計算が面倒なことが多いということです。
入試問題は選抜するテストですから、その意味では学校側に好まれるやり方でしょう。
今後も、計算の繁雑さは無くならないと思われます。
男子校との比較で言うと、根本的に難しいものが好まれるのが男子校、正解することが難しいのが女子校ということになるでしょうか。
分野について見ていくと、最難関の「立体」と「場合の数」についてはある程度難易度を落としているケースが多かったように思います。
この二つの分野に関してはあまり難しすぎると誰もできないということが起こりがちなので、学校側がそうなることは避けているように感じます。
逆に言えば「立体」と「場合の数」についてはいきなり捨ててはいけないということになります。
「捨てる」「捨てない」のボーダーラインは個人差もあってなかなか難しい問題なのですが、今年の桜蔭のⅡ(2)②の「場合の数」の問題ができなければいけないラインの上の方かなと感じました。
この問題がきちんと正解できれば一応合格レベルの力があると思って良いと思います。
参考にしてください。
「立体」に関してはボーダーライン上の問題は見当たりませんでした。
「渋谷幕張」の5(2)は立体が得意ならば解法まではたどり着くでしょうが、その後の計算やどこが何cmなのかといったことで間違えやすいので、結果的には捨てるべきだったというケースが多かったでしょう。
この問題は「時間があればやる」というカテゴリーに入れておきましょう。
前記二分野の次に難問が出る可能性が高いのは「数の性質」でしょう。
前回取り上げた「男子校編」ではこの分野の調べ上げる問題が目につきました。
前回の「今週の1題」と似たようなテーマの問題が「桜蔭」でも出ていました。
本質的にはそんなに難しくないのですが、罠のようなものがあり、正解率はそれほど高くなかったかもしれません。
今年の入試問題で、各学校の特色がいちばん出ていたのは「平面図形」だったのではないでしょうか。
「女子学院」の1.(5)はなかなかの良問だと思います。
基本がしっかりしていないとまず解けないと思いますが皆さんいかがでしょうか。
また、「豊島岡」の5もよくある問題に見えますが、手が止まった受験生も多かったのではないでしょうか。
直感的に解けますが理論を組み上げるのはなかなか大変だと思います。
「フェリス女学院」の3もそんなに難しくはありませんが、意欲的な面白い問題でした。
「渋谷幕張」の4(2)は「算数オリンピック」を思わせるような問題で、今後はそこまで手を広げる必要があるかどうか検討しなければならないでしょう。
以上見てきたように今年は「平面図形」の当たり年だったような気がします。
「速さ」についてはあまり目立ったものはありませんでした。
そんな中「渋谷幕張」の3はやや難問でした。ただ複雑なだけでなく、「最も速い場合」にどのようなことが起こるかをイメージできないと苦しくなる高級な問題でした。
日頃からセンスを磨いておく必要があることを強く感じました。
最後になりますが、どの学校に関してもそれぞれ個別の対策が重要になります。
特に受験する学校の問題のうち「小問」がどれ位の割合を占めるかで対策が変わってきます。
今回で言えばほぼ全て小問の「女子学院」と全て大問の「渋谷幕張」では準備の仕方が全く異なるということです。
※参考までに最も鍛えなければならない能力を記しておきます。
小問が多い → スピード・正確性
小問が少ない → 思考力・書く力
どちらにせよこれらの対策に特化しなければならないのはまだ先のことですので、今は「基本の完成」に専念しましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★☆☆☆
〈図1〉の長方形ABCDは面積が420cm2です。
BE:EC=1:1
AF:FC=2:1
のとき、以下の問に答えてください。
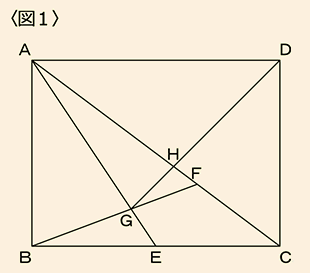
(1)AG:GEをもっともかんたんな整数の比で表してください。
(2)三角形GFHの面積を求めてください。
解答が表示されます













