VOL.334【新シリーズ】中受流証明 ― 整数問題2 ―
今回は「中受流証明」をやってみたいと思います。
どうせならレベルの高い問題に挑戦しましょう。京都大学の入試問題に次のような趣旨の問題があったのでそれを証明したいと思います。
〈問題〉
整数Nを7回掛け合わせたものをN7とあらわします。また,整数Nを7で割ったときのあまりを〈N〉とすることにします。
このとき
〈N〉=〈N7〉
となることを証明してください。
本ブログでも何回か取り上げた「あまりだけを考える」を使えばなんとかなりそうな問題です。ポイントは7で割ったときのあまりは割り切れるときを含め7通りであることです。本問の場合は,そのそれぞれの場合で上の式が成り立っていることが言えればそれで証明できたことになります。
また,「同じ数で割ったときのあまりは,あまりだけを考えれば良い」ということは特に証明せずにそのまま使って良いことにします。
※Nで割ったときのあまりがAという数は「N×M+A」とあらわすことができ,例えばこれに5を掛けた数は「N×M×5+A×5」となります。「N×M×5」の部分はNで割り切れますからあまりが生じるとしたら「A×5」の部分です。これが「あまりだけを考えれば良い」ということの意味です。
例えば「3で割って1あまる数と3で割って2あまる数の積」を3で割ったときのあまりは,
1×2=2を3で割ったときのあまりに等しいので,答は「2」になります。
それでは中受流で証明してみましょう。
〈証明〉
Nを7で割ったときのあまりを0から6の7つに分類します。
1)0
7の倍数ですから7回掛け合わせても7の倍数に変わりなく,あまりは「0」です。
2)1
1を7回掛け合わせても1なので,7で割ったときのあまりは「1」です。
3)2
2×2×2=8 →この時点で3回掛け合わせ
8÷7=1あまり1
1×1=1 → この時点で6回掛け合わせ
1×2=2 → この時点で7回掛け合わせ
2÷7=0あまり2
よって2を7回掛け合わせたものを7で割ったときのあまりは「2」です。
4)3
3×3=9 →この時点で2回掛け合わせ
9÷7=1あまり2
2×2×2=8 →この時点で6回掛け合わせ
8÷7=1あまり1
1×3=3 →この時点で7回掛け合わせ
3÷7=0あまり3
よって3を7回掛け合わせたものを7で割ったときのあまりは「3」です。
5)4
4×4=16 →この時点で2回掛け合わせ
16÷7=2あまり2
2×2×2=8 →この時点で6回掛け合わせ
8÷7=1あまり1
1×4=4 →この時点で7回掛け合わせ
4÷7=0あまり4
よって4を7回掛け合わせたものを7で割ったときのあまりは「4」です。
6)5
5×5=25 →この時点で2回掛け合わせ
25÷7=3あまり4
4×4×4=64 →この時点で6回掛け合わせ
64÷7=9あまり1
1×5=5 →この時点で7回掛け合わせ
5÷7=0あまり5
よって,5を7回掛け合わせたものを7で割ったときのあまりは「5」です。
7)6
6×6=36 →この時点で2回掛け合わせ
36÷7=5あまり1
1×1×1=1 →この時点で6回掛け合わせ
1×6=6 →この時点で7回掛け合わせ
6÷7=0あまり6
よって,6を7回掛け合わせたものを7で割ったときのあまりは「6」です。
整数Nは上の1)から7)までの7つの場合のどれかに必ず当てはまります。1)から7)までの全てで
〈N〉=〈N7〉…①
が成り立っていますから,Nがどんな整数の値をとったとしても,①が成立していることが証明できました。
いかがでしたでしょうか。
7つに分類(実質的には6つ)しなければならないのが少し面倒だったかもしれませんが,小学生でも十分に理解できる内容だったと思います。
今後もレベルの高い問題を取り上げていく予定です。ご期待下さい!
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★★☆☆
1辺が6cmの立方体から何か所かを切り取り,立体Pを作りました。立体Pを〈図1-①〉のように6方向から見ると全て〈図2〉のように見えました。

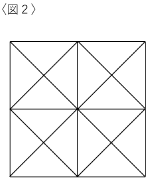
次いで〈図1-②〉で示すA方向から見たものとB方向から見たものが〈図3〉です。
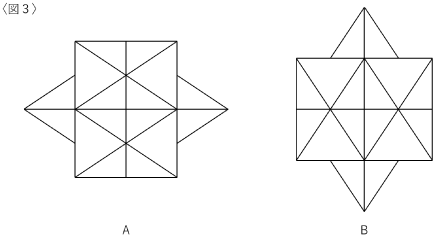
(1)立体Pは全て平面で構成されています。立体Pの面の数を答えてください。
(2)立体Pを立方体から作る際,切り取った部分の体積の合計を答えてください。
解答が表示されます













