VOL.332【新シリーズ】中受流証明 ― 整数問題 ―
前回は、「本人が壁を作ってしまうとそれを越えられなくなってしまう」というお話と、「周りに良い見本があると壁を越えられる」というお話をしました。特に、壁をつくってしまう原因を我々大人が作ってしまうことには注意しなければいけません。
私も今まで以上に気をつけなければならないと気を引き締めているところです。
ところで近年は共通テストの影響か「思考力」を重視する傾向が強くなっているように感じられます。当たり前ですが、自分の力でしっかり考えることができるような人材はどこでも貴重だと思います。当然、中学校側もそのような人材が欲しいはずですが、「勤勉さ」や「努力」を評価する学校も多々あります。「勤勉さ」や「努力」が端的にあらわれたものが「暗記」なので、何か「思考力」と相反するようですが、実際はそんなことはないと思います。
本ブログでは「思考力」の育成は受験のみならず生きる上でとても役に立つものと考え、しっかり伸ばすことを目指してきました。
その一環として新しいシリーズを始めたいと思います。
「中受流証明」です。
年初のあいさつでも「証明」はやるとお伝えしていましたが、やっと始まります。
今回は「1番目からN番目までの立方数の総和は、N番目の三角数の二乗に等しい」ことを中受流で証明したいと思います。
まずは舞台の設定をおこないます。
1辺が1cmの立方体をたくさん用意し、1辺が1個、2個、3個…と1cmずつ大きくなる立方体を次々とつくっていきます。
N=1ならば1辺が1cmの立方体1個をつくり、N=2ならば1辺が1cmの立方体と1辺が2cmの2個の立方体をつくります。立方体をつくった後は、〔それをばらばらにして正方形を作り直すとその1辺がN番目の三角数(cm)になっている〕ということが言えれば、証明できたことになります。
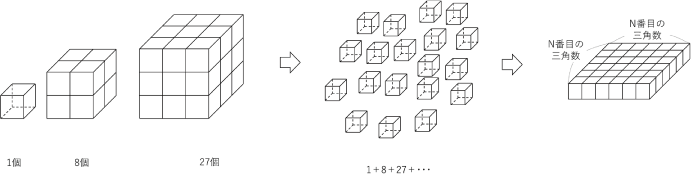
ここでは正方形をつくりそれを使えば立方体ができることを説明したいと思います。
ⅰ)N=1のとき
当然等しいです。
ⅱ)N=2のとき
1×1×1+2×2×2=(1+2)×(1+2)
ⅲ)N=3のとき
正方形で見た時N=2のときの、(1+2)×(1+2)=3×3が(3+3)×(3+3)に増えますから、小立方体は36-9=27(個)増えますが、これは3×3×3なので、1辺3の立方体が作れます。
ⅳ)N=4のとき
正方形の1辺が6cmから4cm増えて10cmになります。このとき増えた面積は10×4の長方形と6×4の長方形です。10は4番目の三角数、6は3番目の三角数でその和は4番目の平方数となることは良く知られています。10×4+6×4を4でくくれば
4×(10+6)となり、かっこ内が4×4になります。結局4×4×4となり立方体をつくれます。
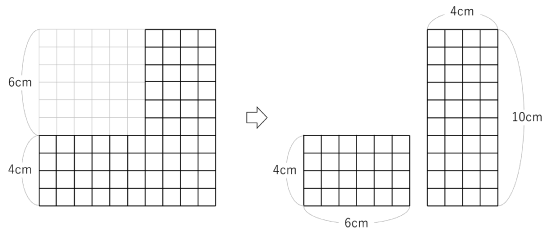
ⅴ)Nのまま考えると
1からN-1のところまでは(N-1)番目の平方数で立方体が作れています。N番目の平方数とその前の平方数との差で1辺がNの立方体がつくれることを示せば証明したことになります。
増える2つの長方形はN×(N番目の三角数)とN×(N番目の1つ前の三角数) なので1辺Nの正方形をN段積むことができます。
※式で書くと
N×(N番目の三角数)+N×(N番目の1つ前の三角数)
=N×(N番目の三角数+N番目の1つ前の三角数)
=N×(N番目の平方数)
=N番目の立方数
ⅰ)からⅴ)までみてきたように、Nが1~4の時は成立し、その後も増えた部分で立方数がつくれるので、いつでも成り立つといえる。
以上で中受流の証明が完成しました。
上の証明では隣の三角数を足すと平方数になることを使っていますが、そこまで証明しようとすると結構な手間になります。「中受流証明」は直感的なものもある程度OKということにします。
これからもやっていくので、皆さんお楽しみに。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★☆☆☆
〈図1〉
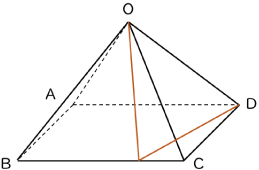
〈図1〉は底面が正方形で側面が正三角形である四角すいOABCDの頂点Oから頂点Dまで辺BCを通るようにひもをピンと張った様子を表しています。
このとき、OからDまでのひもの長さは12cmでした。
つぎに正方形ABCDと合同な正方形4個と正三角形OABと合同な正三角形8個を全て辺と辺を合わせて多面体をつくることを考えます。
多面体をつくるとき、以下のようなルールを設けました。
《ルール》
できた多面体の辺から立方体の12本の辺と同じ位置関係にある辺を12本選ぶことができる。
これについて,次の問題に答えてください。
(1)《ルール》を満たすような多面体は何通りありますか。ただし、回転して重なるものは1通りとみなします。
(2)(1)で求めた多面体の表面積を求めてください。
解答が表示されます













