VOL.330【夏休み】集中学習の準備 ― 基本 ―
今回は本ブログで何回も取り上げている「基本」について考えてみたいと思います。
まずは「基本」の定義ですが,これはいつも書いている「志望校の合格に最低限必要な知識とそれを運用する力」としたいと思います。
「知識」と「力」の土台となる部分が「基本」ということです。
ただし,これに中学受験という前提が加わってくると「合格」が目標になってきますから,〔合格に必要な「基本」〕と,少しハードルが上がるような条件が追加となります。そうなると志望校によって「基本」の範囲が変わってきますね。
一般的に難関校ほど要求される学力のレベルが上がるので,「基本」のレベルもそれなりに上がります。
「基本=簡単」という訳では無いのですね。
但し「基本中の基本」というものも存在しますから,受験生によってはまずそちらから片付けなければならないこともあるでしょう。例えば「分数の計算」「割合の概念」等がわかっていない場合は最優先でそれらをなんとかしなければなりません。
夏休み中に「基本」を完成させることができれば合格への道筋がはっきりと見えてきますから,夏休み前までに「基本中の基本」は完璧にしておく必要があります。
そこで問題になってくるのが「どこまでできているか」の評価です。
「基本中の基本」がまだできていなければ,まずはそこから始めなければなりません。逆にもうできているものをさらに何度も繰り返すようなやり方は効率が悪いでしょう。
この辺りが個別指導のメリットであり,1対1で授業をしていればどんなに小さい穴でも見逃すことなくきっちりとあぶり出し,正すことができます(金田の場合)。
秋以降は過去問演習の結果と擦り合わせをしながら,合格に必要な学力を養成していくわけですが,そのためには夏休みまでにある程度「基本」を固めておかなければなりません。
そして,「基本」を固める絶好の(最後の?)機会が夏休みである以上,その前の段階では「基本中の基本」は完璧にしておきたいのです。
通常は塾のテストの結果を参考に基本ができているかどうかを判断していると思います。特に正答率が50%以上の問題をキチンと正解できているかをチェックするのが得策と言われています。確かにそれには一理あるとは思いますが,間違いの原因は様々なので,無条件に復習というのは効率が悪いかもしれません。
実はこの「穴をみつけて埋める」という部分は講師の腕の見せどころであり,大きく差をつけることができる可能性があります。
ここで少し見方を変えます。
基本には2面あることは何回も書いてきました。1つは「知識」,もう1つは「力」です。
「知識」はやれば誰でも何とかなるのに対して「力」は個人差が大きいようなイメージがあると思います。確かに「力」の養成は難しく,これも腕の差が如実に現れると言えましょう。
では「力」はどうやって身につけるのでしょうか。今からそこに絞って考えてみます。
先程から単に「力」と書いていますが,「持っている知識を使いこなすのに必要な力」というのが正確な表現ですね。
例えば「倍数算の和一定は1本の線分図を描き,比を揃えれば良い」というのが「知識」だとすると,問題を読んで線分図を描き,そこに必要な数値を書き込み,最小公倍数を計算し…というのが「力」ということになるでしょう。つまり,「力」は実際に問題を解くことによって獲得することができるのです。より正確に言えば,問題を解き正解したときに内に秘めた「力」が顕在化し「力」が付いたと実感できることになるのです。そして,正解した(力が付いた)ことによって自信を持ち,次の機会でも「力」を存分に発揮することができ,良い方向に回転していくという訳です。
一方,正解できないとこの逆の現象が起きることがあり,その場合勉強の効率はかなり悪くなってしまいます。
以上より「力」の養成のコツは
・挑戦する機会を十分に与える
・その問題を解くのに必要な知識が備わった状態で挑む
・正解した場合はその勢いを遮らない
・逆に不正解の場合は気持ちを切り替える
・知識が不足していた場合は速やかに補い挑戦の機会を別に設ける
といったことが考えられます。
問題を解く際は極力自分の頭で考え,手を動かし,チャレンジ精神を失わないようにしていただき,「正解」を掴みに行くイメージを強く持ってもらえればと思います。
上のようなことに気をつけて学習を進めていけば,「力」は正解した分,外に現れてきますから,是非積極的に取り組んでもらいたいと思います。
私も皆さんのお手伝いができればと,腕を磨いて待っています!
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
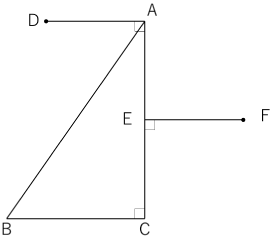
〈図1〉で△ABCは∠C=90°,BC=7cm,AC=10cmの直角三角形です。
また,点Eは辺ACの中点で,∠DAC=∠AEF=90°,DA=EF=5cmです。
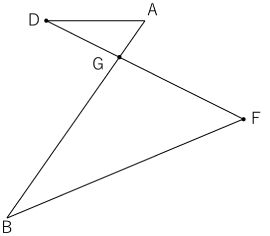
〈図2〉は〈図1〉の点Dと点Fを直線でむずび,ABとの交点をGとしたものです。
〈図1〉
〈図2〉
これについて,次の問題に答えてください。
(1)△DGAと△GBFの面積の差を求めてください。
〈図3〉では,さらに点Dと点Bを結びDH:HB=1:3となるように点Hをとりました。
〈図3〉
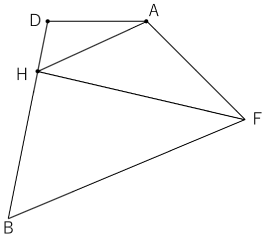
(2)△AHFの面積を求めてください。
解答が表示されます













