VOL.328１問全力解析　2024年度　灘中学校

今回の１問全力解析は2024年灘２日目３です。
まずは問題を見てください。

基本テーマから見ていきましょう。

基本テーマ
①有名三角すいの応用
②体積比を使う
③誘導に乗るための整形
④高さ共通→体積比＝底面積比
⑤砂時計型の相似の舞台をつくる

この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。

①有名三角すいの応用
展開図が正方形になるアレです。立方体の辺の中点２つと頂点を通る面で切り出した三角すいですね。
本問は少し斜めになっていますが，基本的な考え方は同じで良いと思います。
本ブログでも同じような考え方を使った問題がVOL.92の今週の１題にあります。参考にしてください。

②体積比を使う
三角すい台の体積を求める場合は，体積比を使うのが定石です。
引き算方式は計算が煩雑になりやすいのであまりお勧めできません。
受験算数では「比」をうまく使うことが特に重要となります。

③誘導に乗るための整形
誘導が丁寧というか，自動的に乗れるように作ってありますね。
(2)（イ）を解くためには(1)の結果を使う必要があります。そのため通常はそれ用の作図をしなければなりませんが，(2)（ア）を解くために描いた図がそのまま(2)（イ）で使えるようになっています。
相似に気付けば，あとは容易かったでしょう。

④高さが共通な三角すいを使う
図形の問題では特にそうなのですが，複数の解法が考えられることがほとんどです。
なるべく簡明な解法が選べるように普段から感覚を研ぎ澄ましておく必要があります。
高さが共通な三角すいがあればそちらを利用することを是非経験しておきましょう。
単なる知識だと，使えるかどうかは別問題なので，普段から使えるようにトレーニングを積んでおく必要があるでしょう。

⑤砂時計型の相似の舞台をつくる
立体図形はいかに平面に落とし込むかが大切ですが，本問も２つの三角すいに対応する三角形の相似を利用したいところです。
ある平面上で考えればきれいに砂時計型の相似ができますが，皆さんは見つかったでしょうか。

以上を踏まえて問題を解いてみましょう。

(1)正方形からまわりの三角形３個分の面積を引きます。

5×5－（5×3÷2＋5×2÷2＋3×2÷2）＝9.5（cm²）･･･（答）

展開図の直角三角形３つの直角が集まって１つの頂点ができるので
5×3×2×  １  ６  ＝5（cm²）･･･（答）

(2)

(ア)PQとSRは平行なのでPG：GQ＝SK：KR
よって
KS＝3×  １０  １５  ＝2（cm）･･･（答）

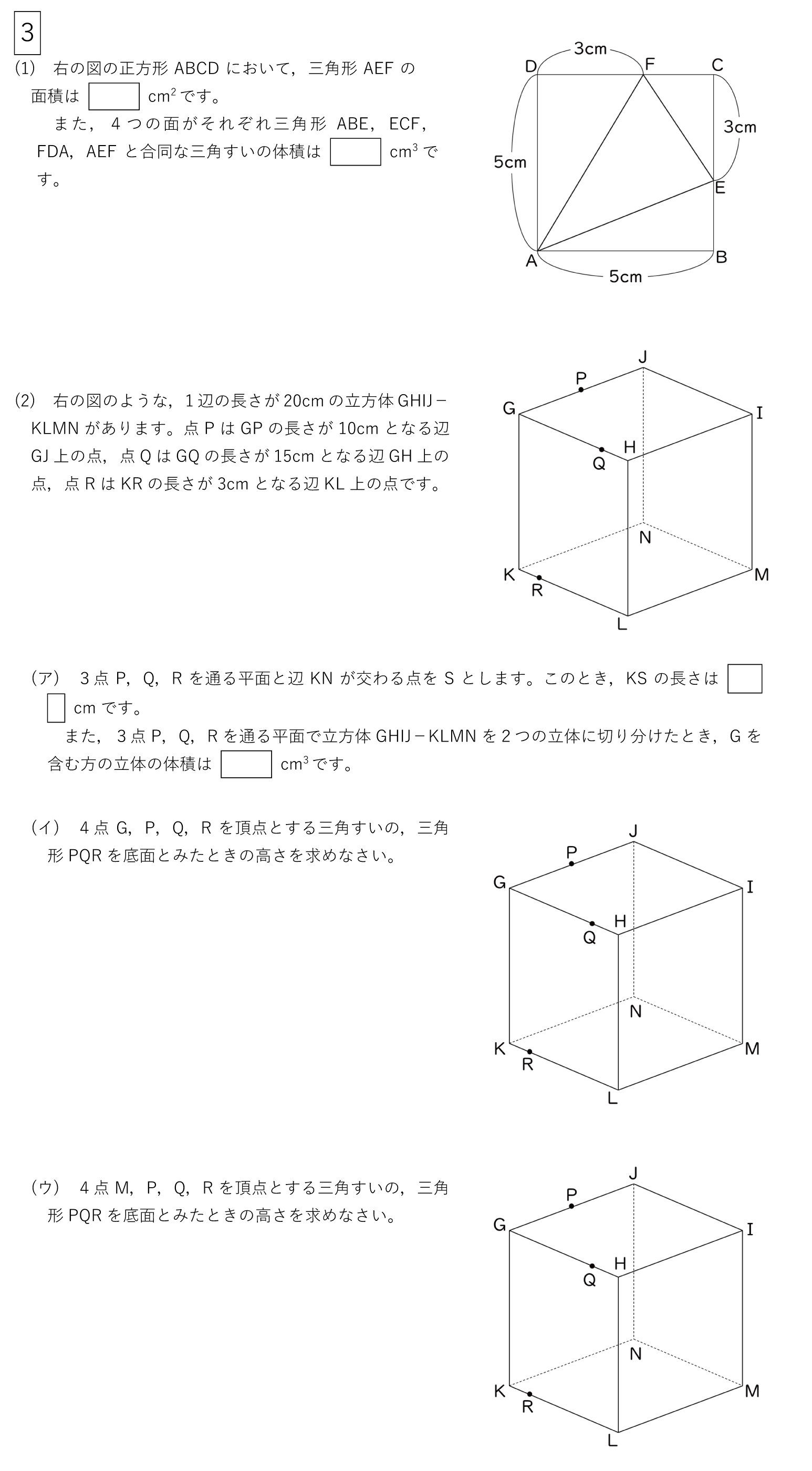
GKを延長して三角すい台を含む三角すいをつくり，その頂点をOとします。（〈図１〉）

〈図１〉

三角すいOGQPと三角すいOKRSの相似比は5：1なので体積比は125：1です。
よって求める体積は
3×2×5×  １  ６  ×(125－1)＝620（cm²）･･･（答）

(イ)求める高さは三角すいOGQPの底面を三角形OPQとみたときの高さと共通です。また三角形OPQは(1)の三角形AEFと相似で，その相似比は５：１です。
よって
620×  １２５  １２４  ×3÷（9.5×5×5）＝７  １７  １９  （cm）･･･（答）

(ウ)三角すいMPQRは，三角すいGPQRと底面（三角形PQR）を共通にしていることに注目します。

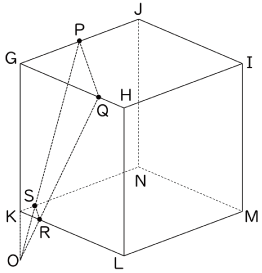
はじめに立方体の上面に注目し，正方形GHIJ上にPQとGIの交点Tをとります。（〈図２〉）

〈図２〉

この時GT：TI＝3：7です。

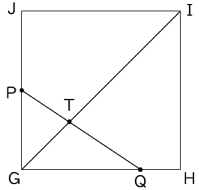
次にG，O，Mを含む平面を考えます。（〈図３〉）

〈図３〉

〈図３〉でGUとUMの長さの比が、三角形PQRを底面としたときの三角すいMPQRと三角すいGPQRそれぞれの高さの比に等しいので

GU：UM＝3：10－3÷5
＝15：47

よって求める答は
７  １７  １９  ×  ４７  １５  ＝２４  １４  １９  （cm）･･･（答）

いかがでしたでしょうか。

まともにやるとかなり厳しかったと思いますが，立体を別の角度から見た図を使えばスッキリ解けたと思います。
他校でもこの考え方を使うと良い問題を見たことがあるので，今後も出題の可能性があると思います。
この機会に技のバリエーションに加えておきましょう。