VOL.3181問全力解析 2024年度 渋谷教育学園幕張中学校
今回の1問全力解析は2024年渋谷教育学園幕張一次4です。
まずは問題を見てください。
基本テーマ
①円周角の定理
②補助線
③相似の発見
④相似→連比
⑤面積比の計算
この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。
①円周角の定理
明らかに中学の範囲ですが、普通に出題されています。これは今後も変わらないと思います。本ブログではお馴染みのテーマですね。
「知っている」で片づけることが出来れば明らかに得です。
②補助線
補助線を引かなければ解けないと思われる問題は以前私が調査したところ、およそ3分の1でした。むやみやたらに補助線を引くことは好ましくありませんが、本問ではピッタリの補助線がありました。
ただし、最低でも2本引く必要があり、図形が苦手な受験生には厳しかったかもしれません。
③相似の発見
(1)では底角の1つを共有している二等辺三角形の相似とピラミッド型の相似、(2)では砂時計型の相似を2組利用して解きます。
二等辺三角形の相似を見抜けないと全く前に進めないので、そこで差がついた可能性があると思います。
④相似→連比
よくある形です。本校の合格レベルに到達していた受験生にとっては一目だったことでしょう。
このタイプの連比は頻出ですから、本校の志望者以外も練習に使ってみると良いと思います。
⑤面積比の計算
本校の特徴でもありますが、解法が分かっている問題は計算が煩雑になることが多いです。
途中はなるべく整数でいくように心がけ、少しでも計算の煩雑さが軽減できるように工夫しましょう。
分母が少し大きい分数になりますが、自信を持って回答欄に答を書き込めるよう、日頃から鍛錬しておきましょう。
以上を踏まえて問題を解いてみます。
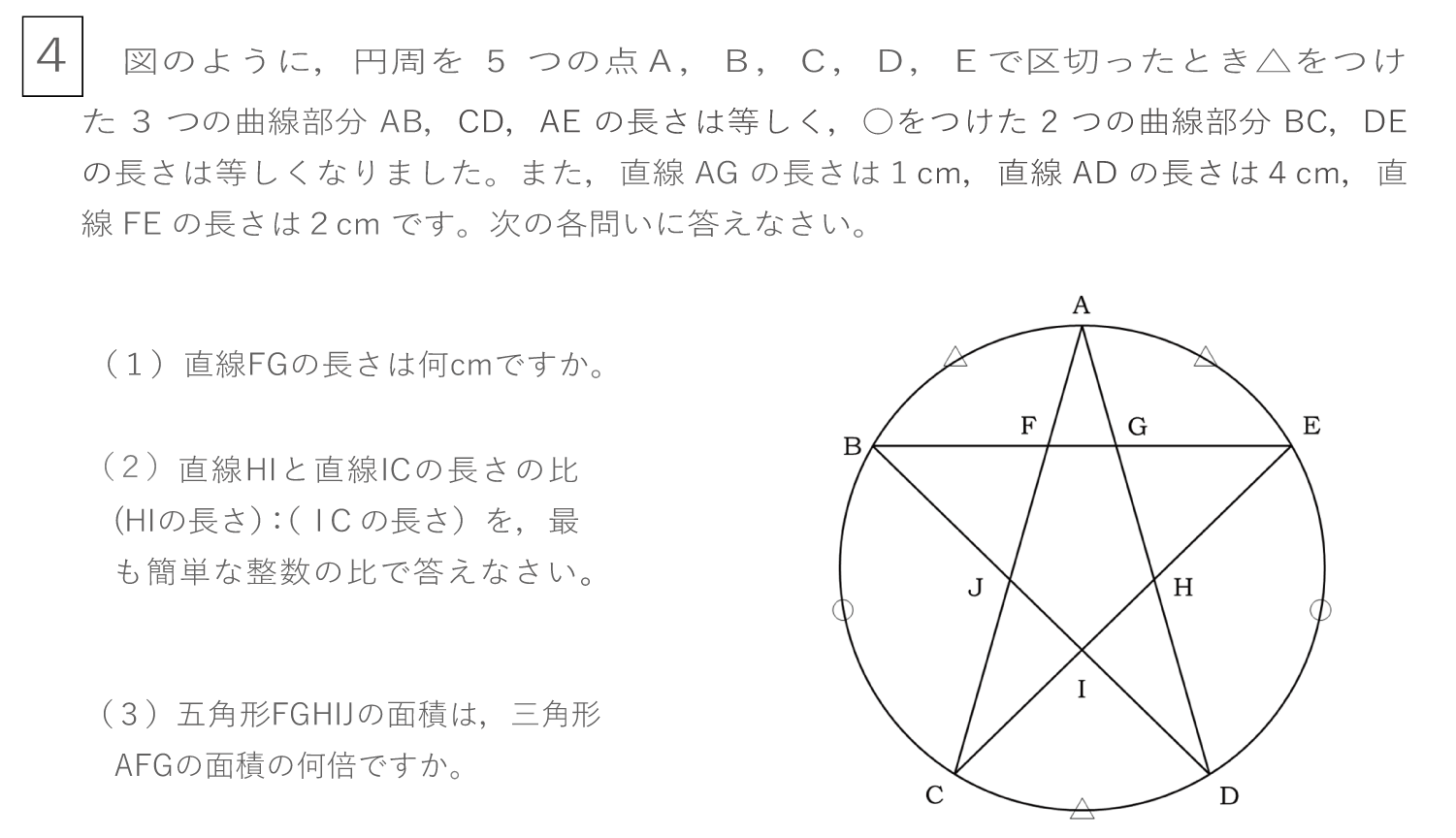
(1)AとE、CとDを結びます(〈図1〉)。
〈図1〉
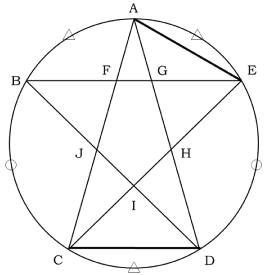
まず押さえておきたいのは△ACDは二等辺三角形であるということです。対称性があるので当然という感覚でよいでしょう。
△ACD≡△CEAも同様です。
また、円周角の定理より∠ACE=∠AEF、∠CAEと∠EAFは共有なので
△CAE∽△EAF
です。
またピラミッド型になっているので(対称性からFG//CDであることは明白)△AFGと△ACDも相似です。
△AEFは二等辺三角形なのでAE=2cm=CD
△ACDと△AFGの相似比は4:1なので
FG=2× 1 4 =0.5 (cm)…(答)
(2)〈図1〉で2つの砂時計型の相似が見えれば、その連比で解決です。
△IBE∽△IDC→相似比は2×2-0.5:2=7:4
△HGE∽△HDC→相似比は2-0.5:2=3:4
ECを77とおけば
EH=33,HI=44-28=16、IC=28
なので
HI:IC=16:28
=4:7…(答)
(3)△AFGの面積を1とすると△FCEの面積は3×4=12となります。
△EGHは
12× 3 4 × 3 7 =3 6 7
△CIJは
12× 4 11 × 4 7 =2 38 77
五角形FGHIJは
12-(3 6 7 +2 38 77 )=5 50 77 となり、これがこのまま答です。
(答) 5 50 77 倍
いかがでしたでしょうか。
全く手をつけることができなかった受験生もいたかもしれませんが、相似(合同)と比を上手く利用できれば、攻略も可能だったことでしょう。
対称性を考慮すれば結論が明白な部分もあったので、それも利用したかったところです。
もはや、円周角の定理は常識なのか、と思わせるような問題でした。
当ブログの読者にとってはお馴染みだったので、良いことがあったかもしれません。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★☆☆☆
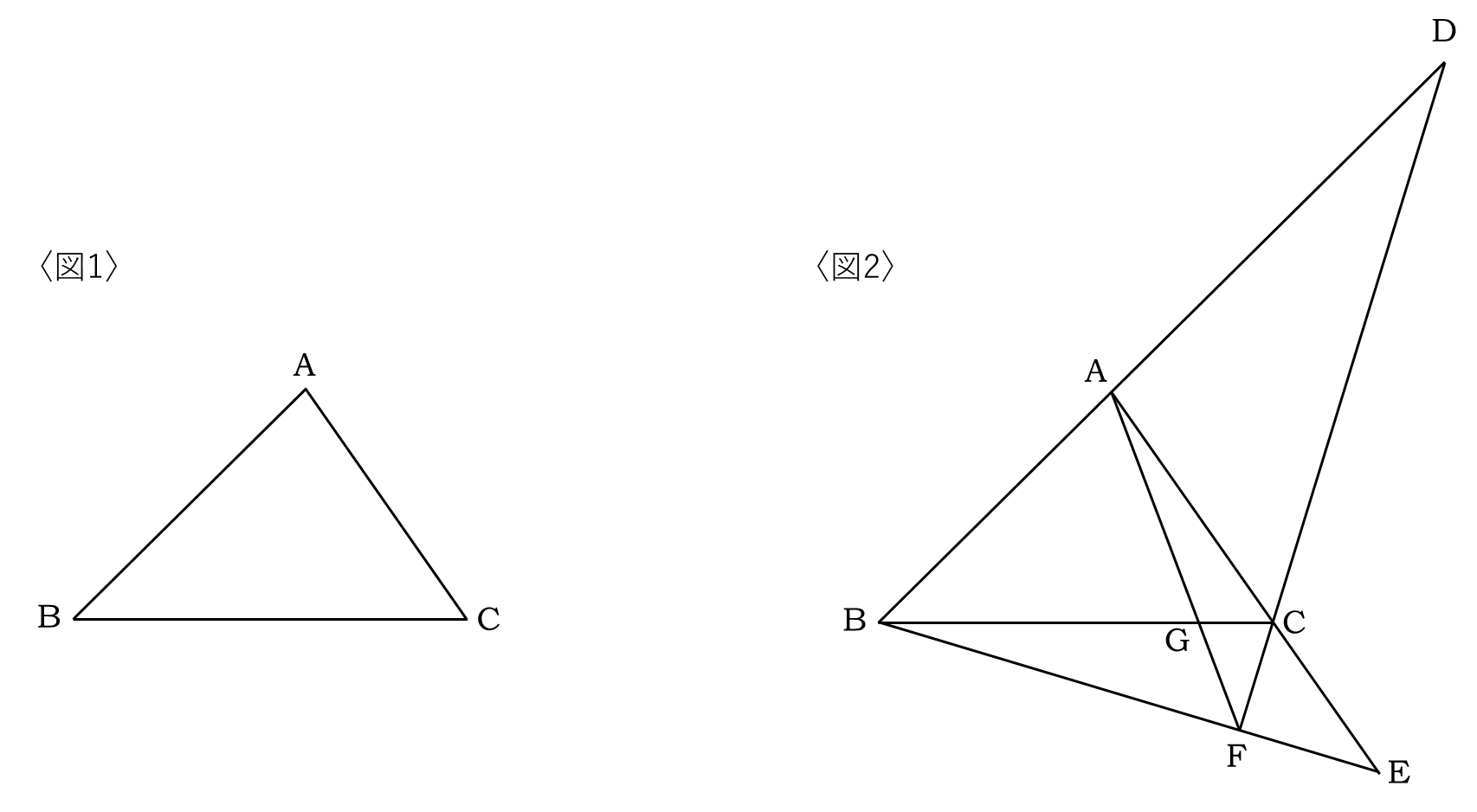
〈図1〉の三角形ABCのBAとACの延長線上にそれぞれ点Dと点Eをとり、〈図2〉のように結びました。
BG:GC=9:2
AC:CE=5:3のとき
次の問に答えてください。
(1)DA:ABを求めてください。
(2)三角形AGCと三角形ACDの面積比を求めてください。
解答が表示されます